Alex's Notes

cm3015 Topic 03: Regression

Main Info

Description

In this topic we will discuss linear regression, a simple technique for fitting data in a linear manner. We introduce gradient descent, one of the most important algorithms used in training machine learning models, and show how this can be applied to real-world data.

Week Five: Linear Models.

Week Six: Gradient Descent, applications.

Assigned Reading

Linear Algebra

Gradient Descent

Further Reading (Unassigned)

Lecture Summaries

3.102: Linear Regression

Linear regression involves predicting some output based on a linear combination of the input. We fit a line to our data.

The line is defined by two parameters: \(\theta_0\), the intercept (or bias), a constant, and \(\theta_1\) the gradient.

We can express this mathematically as: \(h_\theta (x) = \theta_0 + \theta_1 x_1\) or as a summation:

\[h_\theta (x) = \sum^1_{j=0} \theta_j x_j\]

With \(x_0 = 1\). Then we could add additional parameters.

Or in vector notation:

\[ = \begin{bmatrix} 1 & x_1 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix}\]

Introduces the independent and dependent variable terminology. Suggests plotting your variables to visually inspect relationships.

We start with a hypothesis, could be a random line, then we measure the distance between the data and the line, or the loss.

One measure is the L2 loss or the mean squared error:

\[J(\theta) = \frac{1}{2m} \sum^m_{i=1}(h_\theta (x^{(i)}) - y^{(i)})^2\]

Squaring ensures the loss is always positive. We then try to minimize this loss. Next lecture will cover the algorithm to do this.

3.301 and 3.302: Gradient Descent

Recaps L2 loss, plots a convex loss function. Introduces gradient descent, moving in the opposite direction of the gradient. When the slope is flat we’ve found our minimum. So we need to calculate the gradient at any point of the loss function. Time for calculus! Shows with one dependent variable, that the gradient of L2 loss above is, simplifying to just focus on \(\theta_1\):

\[J_1’(\theta) = \frac{\partial J(\theta)}{\partial \theta_1} = \frac{1}{m} \sum^m_{i=1} \left( \theta_0 + \theta_1 x_1^{(i)} - y^{(i)} \right) \times x_1^{(1)}\]

So how does gradient descent work? We calculate the gradient of the loss function at a particular point, then update the weights by subtracting that gradient multiplied by an \(\alpha\) value, or learning rate, also called convergence rate. If the slope is steep we’ll move far, if it tailing off, then we are getting close to a minimum. If \(\alpha\) is too big it will not converge, it will jump back and forth around the minimum, if it is too small it will take far too long. So setting the alpha is important.

This only works if the loss function is differentiable and has a global minimum.

Next lecture switches to accommodate \(\theta_0\) as well. Now we need to update the gradient equation to include the second dimension. The partial differential for the bias variable is almost the same, but there is no x to multiply at the end:

\[J_1’(\theta) = \frac{\partial J(\theta)}{\partial \theta_0} = \frac{1}{m} \sum^m_{i=1} \left( \theta_0 + \theta_1 x_1^{(i)} - y^{(i)} \right)\]

The additional dimension means the loss, instead of being a flat curve, is more like a bowl. Gradient descent can scale to multiple dimensions. We update the parameters in parallel by subtracting the gradient as before until convergence.

This is batch gradient descent, using all the data on each iteration. It can be slow if you have a lot of data as each iteration you calculate the loss over all data.

An alternative is stochastic gradient descent where you choose a random data item on each iteration to calculate the loss for that round. The advantage of this is that it’s much faster. The disadvantage is that it doesn’t converge smoothly, the gradient can be erratic.

A hybrid is mini-batch gradient descent, where you take a random subset, rather than just one point.

Shows how linear model scales nicely adding new features to the model, which is just adding another feature. This gives us a multivariate linear model. The bias remains when you scale up like this, and is never multiplied.

3.305: Data Scaling

There are issues with multiple variables, especially scaling. Imagine a dataset where different features have very different scales. You might have a boolean 1,0 parameter, while another is in the millions. This means that the corresponding weights can be very different in scale too.

One step we usually do is to scale or normalize. We might do this through min-max normalization where all data is made to fit within the range (0,1):

\[x_j^s = \frac{x_j - \mathrm{min}(x_j)}{\mathrm{max}(x_j) - \mathrm{min}(x_j)}\]

Sometimes this is essential for gradient descent. Convergence can be much faster.

There are other techniques, including range normalization, centered on the mean, doesn’t force between 0 and 1, works well with normal distribution of data:

\[x_j^s = \frac{x_j - \mathrm{mean}(x_j)}{\mathrm{max}(x_j) - \mathrm{min}(x_j)}\]

Another is standardization (z-score), again for normally distributed data:

\[x_j^s = \frac{x_j - \mathrm{mean}(x_j)}{\mathrm{std}(x_j)}\]

Need to look at pros and cons outlined in the literature and see what suits your dataset best.

3.306: Polynomial Regression

A line doesn’t always fit the data well of course. One trick is to add more features. We don’t introduce new variables, but manipulate the existing variables (eg square them). This can complicate the line and fit the data better:

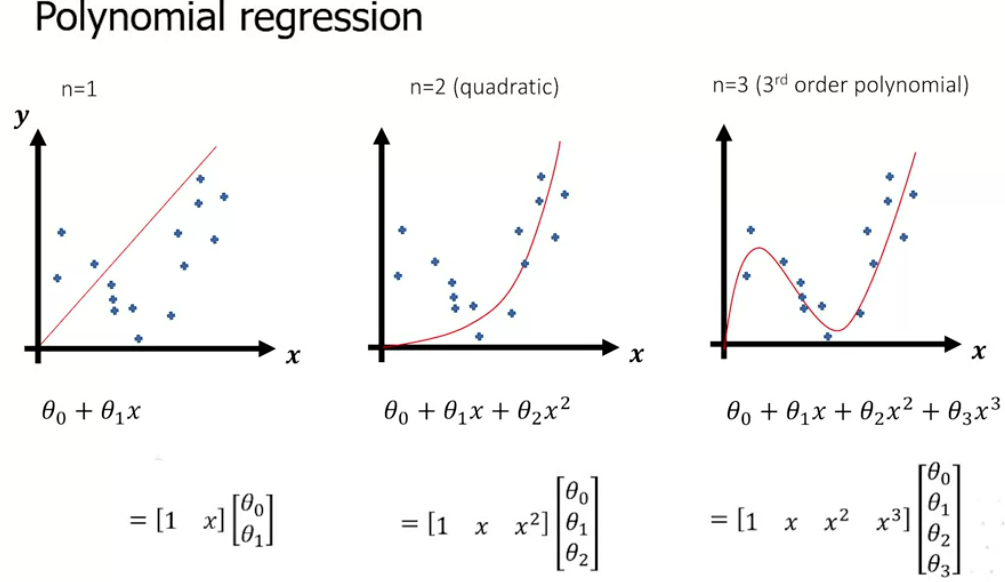
It’s still a linear equation, but we’ve made the data nonlinear. It’s non-linear in x, but the parameter space is still linear, so gradient descent can be used. Not limited to just squaring the data, can root them etc.

Lab Summaries

Lab One: Linear Algebra with Numpy. Involves matrix manipulation (see Numpy Linear Algebra Cheatsheet)

Lab Two: Linear Regression with Scikit-learn shows this example and asks you to adapt it to different datasets.

Lab Three: The most involved lab, implement linear regression and gradient descent in two dimensions from scratch to test against the linear regression method built into SKL. Solution is here: cm3015 Lab03: Gradient Descent

For datasets see the scikit-learn datasets page

Links to this note