Alex's Notes

cm3015 Topic 06: Unsupervised Learning

Main Info

Description

This topic introduces two fundamental types of unsupervised machine learning algorithm. The first is clustering: given a set of data, the goal of the algorithm is to provide groupings of subsets of the dataset in order to capture some interpretable qualities. As an example of this, we will implement the k-means clustering algorithm. The second type of unsupervised learning is dimensionality reduction. Here we will briefly discuss one of the most commonly used algorithms for reducing the dimensions of data: principal component analysis (PCA).

Key Reading

Other Reading

Lecture Summaries

6.101 Intro

Supervised learning is the dominant method, but can’t be applied everywhere. Depends on costly and error-prone process of human labelling. Unsupervised labeling comes in here - analysis of data without labels.

Focuses on clustering and dimensionality reduction. Clustering is an unsupervised method of separating a set of data into subgroups. It helps find ‘inherent’ groups in the data.

Dimensionality reduction - given a high dimensional dataset we want to reduce this to a lower-dimensional embedding without losing useful information - discarding noise but preserving information. Principal Component Analysis (PCA) is one method of doing this that we’ll look at.

Clustering

6.102 Clustering

The goal of unsupervised learning is to learn patterns in the data without the benefit of labels.

In a supervised world, the labels provided constrain the space of valid hypotheses. But in unsupervised learning we need some other constraint. The choice of constraint depends on the specific task we’re interested in.

We want to map our input observations X to our output values Y, they need to satisfy some constraint. Perhaps the constraint is a measure of similarity, where we map observations that are similar in X to outputs that are similar in Y. Alternatively the constraint could be finding ways of reducing the size of X (its dimensionality) while maximizing the variance between the data points once we get to our mapping in Y. This is dimensionality reduction.

Shows an example dataset, and how it might be clustered using k-means clustering into various clusters depending on the choice of k.

6.103 K-means Clustering

How does k-means work? Let’s look at a single variable example. We could take a mean or standard deviation. But there might be clear groupings which these aggregates would ignore. These groupings are what k-means finds automatically.

Walks through the k-means algorithm:

  1. Initialise k centroids (randomly) - a random point in space.

  2. Calculate the distance from each centroid to every data point.

  3. Assign data points to their nearest centroid to form initial clusters.

  4. Re-assign the centroids as the mean of each cluster’s data.

  5. Repeat steps 2-4 until we reach convergence (centroids stop changing).

The issue with this, is that it’s subject to local minima, depends on your initial choice of centroid locations. So you need to choose good initial centroids. You can restart with different centroids several times.

Essential to scale the data before you run k-means on it if you have multi-dimensional data. Large values can dominate the other dimensions.

You can do min-max scaling with the function \(x = (x - \mathrm{min}(x)) / (\mathrm{max}(x) - \mathrm{min}(x))\)

Dimensionality Reduction

6.302 Dimensionality Reduction

Particularly useful with images. Take a 640 x 480 pixel picture. Each pixel is a dimension, so we have some 300,000 features/dimensions. Solution: map to a lower dimensional space. We want this embedding to capture the important parts of input, using latent features that we might not observe directly.

One of the most common algorithms is Principle Component Analysis. We want to preserve the variance in the data while reducing the dimensions. Where is the most variability? We find the axis along which there is the most variation from the mean. And then we find an orthogonal axis which has the next most variation. Now we’ve created our first two principal components. Then we rotate the space to make the axes define the space:

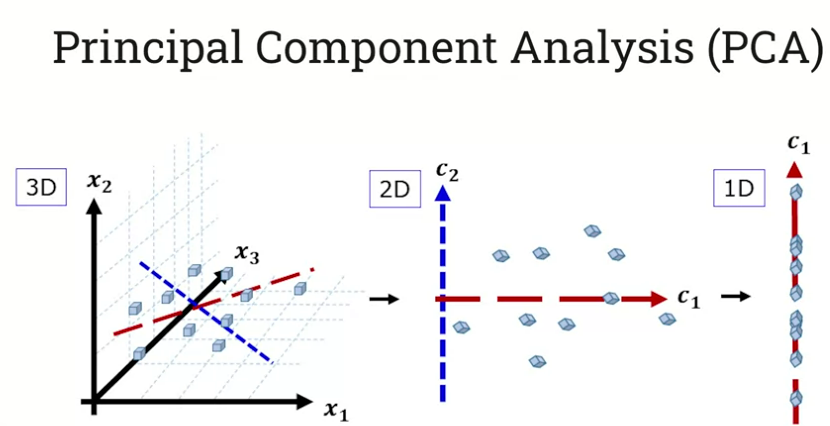
We lose some information, but retain enough to preserve the ‘essence’ of the data.

6.303 PCA

Digs into the algorithm:

Given data X with F features and N samples:

\[\mathbf{X} = [\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \dots , \mathbf{x}^{(N)}]\]

The sample mean is then:

\[\mathbf{\bar{x}} = \frac{1}{N}\sum^N_{i=1}\mathbf{x}^{(1)}\]

The covariance is:

\[cov(\mathbf{X}) = \mathbf{S} = \frac{1}{N}\sum^N_{i=1} \left(\mathbf{x}^{(1)} - \mathbf{\bar{x}} \right) \left(\mathbf{x}^{(1)}-\mathbf{\bar{x}} \right)^T\]

Covariance captures how the N variables vary together, change together with respect to the mean.

The basic premise of PCA is that we’re trying to do a linear projection: a linear transformation from one dimension to another. The PCA matrix W maps data X onto Y: \(Y = W^TX\).

The key question then is how do we learn W? The criteria is that we want to maximize the covariance of the output:

\[cov(Y) = cov(W^TX) = W^Tcov(X)W\]

If for notational convenience we say \(S = cov(X)\) then we have the challenge to find the W that maximizes \(W^TSW\).

So why not set W to infinity? We have to add a constraint that W times its transpose is the identity matrix. This also ensures that the projected features are linearly independent, so the axes are orthogonal.

We can use eigenanalysis to get the optimal values of W.

\[eig(S) = [W,\Lambda]\]

Where \(S = cov(X)\), \(\Lambda\) is the eigenvalues, and W is the eigenvectors.

Here’s the procedure for PCA with Eigenanalysis:

  1. Centre data around the mean, ie \(X = X - \bar{X}\)

  2. Calculate the covariance matrix \(S = cov(X)\)

  3. Calculate the eigenvalues and eigenvectors, \([\mathbf{W}, \Lambda] = eig(S)\)

  4. Order the eigenvalues from large to small - for a 2D output, keep the 2 eigenvectors from W that correspond to the 2 biggest eigenvalues. This is \(\mathbf{W_2}\)

  5. Project the original data by multiplying \(\mathbf{W_2}\) with X, so \(Y = \mathbf{W_2}^TX\)

Shows an example using this for data compression.

Ends with an example, how could we compress three linearly dependent sine waves? We could compress to a single dimension and still reverse.

Lab Summaries

Clustering

The clustering lab has you walk through the process of k-means clustering the iris dataset in skl and using the clusters as labels for a supervised training algorithm.

PCA

The PCA lab is not an exercise, it just has you read through an example of using it on a face dataset to perform facial recognition. The results are precise but the recall is terrible.

Links to this note