Depth-limited and iterative Deepening Search

As outlined in Russell Norvig Chapter 03: Solving Problems by Searching

Definition

A Search Algorithm that adopts an Uninformed Search Strategy:

To keep Depth-first Search from wandering down an infinite path, we can use depth-limited search, a version of depth-first search in which we supply a depth limit, l, and treat all nodes at depth l as if they had no successors. (p. 98)

The choice of l is clearly critical, a poor choice will mean the algorithm fails to reach a solution, making it incomplete.

Sometimes a good depth limit can be chosen based on knowledge of the problem. For example, if we study the state space we might see its diameter, that is the maximum number of edges/actions between any two nodes/states. This will give us a more efficient search process. Often we don’t know the best depth limit until we solve the problem though.

Implementation

Iterative deepening search solves the problem of selecting a good value for l by trying all values, until either a solution is found, or depth-limited search returns failure rather than cutoff.

In general, iterative deepening is the preferred uninformed search method when the search state space is larger than can fit in memory and the depth of the solution is not known. (p. 100)

Pseudocode

For depth-limited search:

For iterative deepening search;

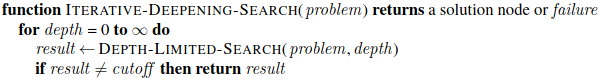
Properties and Performance

Iterative deepening combines many of the benefits of breadth-first and depth-first search. Modest memory requirements, optimal for problems where actions have the same cost, complete on finite acyclic state spaces (or any space where we check for cycles).

Its memory requirements are \(O(bd)\) where there is a solution or \(O(bm)\) where there is no solution.

The time complexity is \(O(b^d)\) where there is a solution, and \(O(b^m)\) where there is no solution. Whereas breadth-first search generates new levels in its search tree by storing prior levels in memory, iterative deepening does so by regenerating the previous levels from scratch in a new iteration. Thus it saves memory at the cost of time.

This may seem wasteful, but for many state spaces most of the nodes are in the bottom level, so it does not matter much that the upper levels are regenerated. In an iterative deepening search the bottom level nodes are generated once, the next level twice and so on. This ends up giving the same asymptotic complexity as breadth-first search (p. 99).