Minimum Edit Distance (Jurafsky Martin)
Definition and Introduction
Edit distance gives us a way to quantify… intuitions about string similarity. More formally, the minimum edit distance between two strings is defined as the minimum number of editing operations (operations like insertion, deletion, substitution) needed to transform one string into another.
Edit distance is used a lot in NLP. For example in spelling correction tasks, and to identify coreference where two strings refer to the same entity.
An important visualization for edit distance is an alignment between two strings, which shows the correspondence between substrings of the two sequences, along with an operation list, like the following (where d is deletion, i insertion, and s substitution):
| I | N | T | E | * | N | T | I | O | N |
| * | E | X | E | C | U | T | I | O | N |
| d | s | s | i | s |
We can assign costs or weights to these operations. The Levehnstein distance is the simplest weighting factor where every operation costs 1, except where a letter is substituted for itself, which costs 0. There is an alternative Levehnstein metric where each operation costs 1 but substitutions are not allowed, so substitutions effectively cost 2 (a deletion and insertion).
The algorithm
The space of all possible edits is enormous so we can’t do a naive search. A lot of edit paths will end up in the same state, so we can remember the shortest path to a particular state rather than recompute it every time. This is an application of dynamic programming, a class of algorithms where a table is used to store solutions to sub-problems, which are then combined to give the overall solution. Dynamic programming is also used a lot in NLP, eg the Viterbi algorithm, and CKY parsing algorithm, discussed later.
Intuitively, imagine some state (or string) on the optimal path. Then the optimal sequence must also include the optimal path from the source to that state. Otherwise if there were a shorter path we could use it to create an overall shorter path.
We can formally define the edit distance between two strings:
Given two strings, the source string \(X\) of length \(n\), and target string \(Y\) of length \(m\), we define \(D[i,j]\) as the edit distance between \(X[1..i]\) and \(Y[1..j]\), ie the first \(i\) characters of \(X\) and \(j\) characters of \(Y\).
As base cases, let the source have \(i\) characters, and the target 0. Then we require \(i\) deletions so the edit distance is \(i\). And let the source have 0 characters and the target \(j\), then we require \(j\) insertions, for an edit distance of \(j\).
We can use these base results to start building out a matrix based on previously computed results. Hereafter \(D[i,j]\) is computed by taking the minimum of the three possible paths through the matrix to arrive at that location:
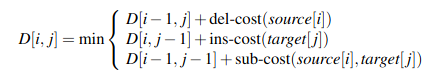
Or with Levehnstein distance values used (with substitutions costing 2):
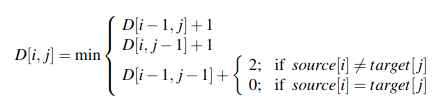
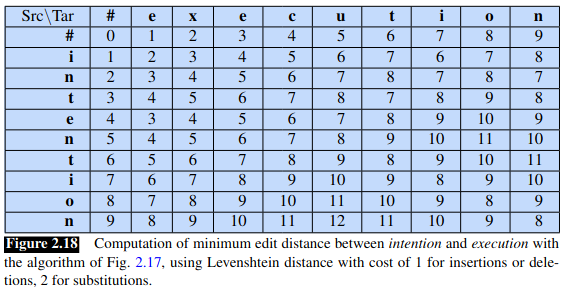
This gives us the following algorithm:

and the following worked example:
Alignment
The algorithm is not just helpful for spelling errors, it gives us the minimum cost alignment between two strings. This is used throughout speech and language processing, such as machine translation and speech recognition.
To extend the algorithm, we simply store in each cell of the matrix ‘backpointers’ that show the cell we came from. To create the alignment, we can then start in the final cell and trace the route back to the beginning. Each complete path back to the initial cell is a minimum distance alignment.
This can be seen in the chapter’s visualization:
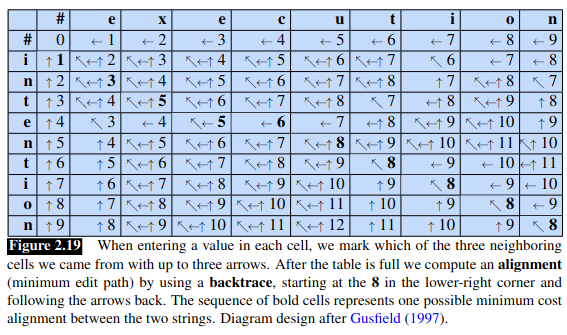
The Viterbi algorithm extends this idea by introducing probability to describe a “maximum probability alignment”. This is covered in chapter 8.