Jurafsky Martin Chapter 05: Logistic Regression
Metadata
Title: Logistic Regression
Number: 5
Summary
This chapter introduces the logistic regression model of classification:
Logistic regression is a supervised machine learning classifier that extracts real-valued features from the input, multiplies each by a weight, sums them, and passes the sum through a sigmoid function to generate a probability. A threshold is used to make a decision.
Logistic regression can be used with two classes (e.g., positive and negative sentiment) or with multiple classes (multinomial logistic regression, for example for n-ary text classification, part-of-speech labeling, etc.).
Multinomial logistic regression uses the softmax function to compute probabilities.
The weights (vector w and bias b) are learned from a labeled training set via a loss function, such as the cross-entropy loss, that must be minimized.
Minimizing this loss function is a convex optimization problem, and iterative algorithms like Gradient Descent are used to find the optimal weights.
Regularization is used to avoid overfitting.
Logistic regression is also one of the most useful analytic tools, because of its
ability to transparently study the importance of individual features.
Introduction and Comparison with Naive Bayes
Introduces logistic regression, “one of the most important analytic tools in the social and natural sciences”. Focuses on binary logistic regression, only briefly introducing multinomial logistic regression for more than two classes.
Distinguishes again between generative classifiers like Naive Bayes and discriminatory classifiers. A generative model has the goal of understanding, for example, what dogs and cats look like, such that you could ask it to draw a dog. In a discriminatory classifier, the model only learns to distinguish between the two classes. So long as it can do that, it’s satisfied, so eg if all dogs wear collars in the training set, and no cats do, the discriminative model might conclude that the collar is the key discriminant and be done.
Logistic regression has a number of advantages over naive Bayes. NB has overly strong conditional independence assumptions. Consider two strongly correlated features (like if \(f_1\) occurs twice), NB will treat both copies as separate, multiplying them both in and overestimating the evidence. Logistic regression is much more robust to correlated features. Logistic regression generally works better on larger documents and is a common default.
NB can work very well on small datasets or short documents however, and it is easy to implement and very fast to train. So can still be a reasonable choice in some situations.
Like NB, logistic regression is a probabilistic classifier, in the class of supervised ML classifiers. ML classifiers require a training set of m input/output pairs: \((x^{(i)},y^{(i)})\). The system has four components:
A feature representation of the input. For every x(i) this will be a feature vector: \([x_1,x_2,\dots , x_n]\). For a specific input x(j) feature i might be denoted \(x_i^{(j)}\), or \(x_i\), \(f_i\), \(f_i(x)\), or \(f_i(c,x)\) in multiclass cases.
A classification function that computes \(\hat{y}\), the estimated class, via \(p(y|x)\). JM introduce the sigmoid and softmax tools.
An objective function for learning, usually minimizing error on training examples. JM use the cross-entropy loss function.
An algorithm for optimizing the objective function. JM intro the stochastic gradient descent algorithm.
The Sigmoid
The sigmoid is a function that takes a real-valued number and maps it into the range [0,1], ie to a probability range. It is nearly linear around 0 but flattens towards the ends, squashing outliers toward 0 or 1. It’s also differentiable, which means it can be used for learning.
Given a feature vector \([x_1,x_2,\dots , x_n]\) the binary classifier output can be 1 (meaning the observation is a member of the class) or 0 (not a member). We want to know the probability \(P(y=1|x)\).
Logistic regression solves this task by learning, from a training set, a vector of weights and a bias term.
Weights: Each weight \(w_i\) is a real number, associated with one of the input features \(x_i\). The weight represents how important the feature is to the classification decision. It can be positive (provides evidence that the instance belongs in the positive class) or negative (evidence for belonging in the negative class).
Bias term: The bias term, also called the intercept is another real number that’s added to the weighted inputs.
So to make a decision on a test instance we multiply each feature by its weight, sum them, then add the bias term b. This gives us the weighted sum of the evidence, z:
\[z = \left( \sum^n_{i=1} w_ix_i \right) + b\]
We can express this in linear algebra terms using the dot product notation:
\[z = w \cdot x + b\]
Note that z could be in the range \((-\infty , \infty)\). To create a probability we need to pass z through the sigmoid function, also called the logistic function, which gives logistic regression its name. The sigmoid is denoted \(\sigma (z)\), and has the following equation:
\[\sigma (z) = \frac{1}{1+e^{-z}} = \frac{1}{1+ \exp (-z)}\]
Graphically:
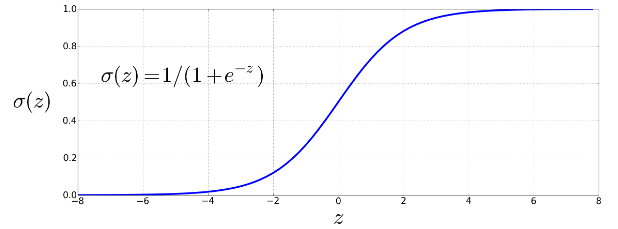
To make a classification decision, we can say that .5 will be the decision boundary, and that if \(P(y=1|x) > 0.5\) the classification is 1, otherwise 0.
Designing Features
As with Naive Bayes, features aren’t limited to bag of words representations. Here are some example features JM show for sentiment classification:
| Var | Definition |
|---|---|
| \(x_1\) | count(positive lexicon words in the doc) |
| \(x_2\) | count(negative lexicon words in the doc) |
| \(x_3\) | 1 if “no” in doc, 0 otherwise |
| \(x_4\) | count(1st and 2nd pronouns in doc |
| \(x_5\) | 1 if “!” in doc, 0 otherwise |
| \(x_6\) | log(word count of doc |
Note that, eg \(x_2\) can be given a negative weight. Logistic regression is used for all sorts of NLP tasks. Eg in period disambiguation we might have features relating to whether the current word is upper or lower case, and whether the next word is upper or lower case:
| Var | Definition |
|---|---|
| \(x_1\) | 1 if \(Case(w_i)\) is lower, 0 otherwise |
| \(x_2\) | 1 if \(w_i\) is in our acronym dictionary, 0 otherwise |
| \(x_3\) | 1 if \(w_i\) = “St.” and \(Case(w_{i-1})\) is upper, 0 otherwise |
Features are generally designed by examining the training set with an eye to linguistic intuition and the linguistic literature on the domain, along with careful error analysis on the training set and devset.
For some tasks it can be very helpful to build complex features that are combinations of more primitive ones (like the “St.” example above). These combination features or feature interactions have to be designed by hand in logistic regression or Naive Bayes.
For many tasks we’ll need large numbers of features. These are often created automatically via feature templates, abstract specifications of features. For example, a bigram template might create a feature for every pair of words that occurs before a period in the training set. So the feature space is sparse. A feature is generally created as a hash from the string descriptions.
Recent work has focused on representation learning to avoid the huge human effort in feature design.
Learning in Logistic Regression
The chapter then discusses the learning process in detail. This spans cross-entropy loss and gradient descent both important topics for other modules too and so split into a separate note. See more detail at Learning in Logistic Regression and the notes on Gradient Descent and Regularization.
Multinomial Logsitic Regression
If we have more than two classes (for example a sentiment classifier that includes ‘neutral’, or a part of speech tagger, or a named entity type recognizer), then we use multinomial logistic regression, also called softmax regression.
In multinomial logistic regression the target y is a variable that ranges over more than two classes; we want to know the probability of y being in each potential class \(c \in C\), \(p(y = c|x)\).
The multinomial logistic classifier uses a generalization of the sigmoid called the softmax function to compute \(p(y=c|x)\). Softmax maps a vector \(z=[z_1,z_2,\dots , z_k]\) of k arbitrary values to a probability distribution where each value is in the range \((0,1)\) and the sum of all values is 1. For a vector of dimensionality k, softmax is defined as:
\[\mathrm{softmax}(z_i) = \frac{\exp (z_i)}{\sum^k_{j=1} \exp (z_j)} 1 \leq i \leq k\]
The denominator normalizes all the values in the output vector to probabilities, squashing values toward 0 or 1. Where \(z=[z_1,z_2,\dots ,z_n]\) the output is a vector:
\[\mathrm{softmax}(z) = \left[ \frac{\exp (z_1)}{\sum^k_{i=1} \exp (z_i)}, \frac{\exp (z_2)}{\sum^k_{i=1} \exp (z_i)}, \dots , \frac{\exp (z_n)}{\sum^k_{i=1} \exp (z_i)} \right]\]
Like the sigmoid, the input will be the dot product between the weight and input vectors, plus a bias. But now we’ll need separate vectors for each of the K classes:
\[p(y=c|x) = \frac{\exp (w_c \cdot x + b_c)}{\sum^K_{j=1} \exp (w_j \cdot x + b_j)}\]
Features in Multinomial Logistic Regression
We now need separate weight vectors (and biases) for each of the K classes. A feature can be evidence for or against each individual class, and can be weighted accordingly. So weights are dependent on both the input and the output class, and this can be made explicit by representing them as \(f(x,y)\), a function of both input and class, eg \(f_5(x,+)\),\(f_5(x,-)\),\(f_5(x,0)\) in sentiment classification with three classes.
Learning in Multinomial Logistic Regression
The loss function generalizes the loss function for binary logistic regression from 2 to K classes. The loss function for a single example x is the sum of the logs of the K output classes, each weighted by \(y_k\), the probability of the true class. The vector y is a one-hot vector since the probability is 1 for the correct class, and 0 for everything else.
The gradient for a single example turns out to be similar to the gradient for binary logistic regression, the difference between the value for the true class k (ie 1) and the probability the classifier outputs for k, weighted by the value of the input \(x_i\).