Chollet: Chapter 02: Mathematical Building Blocks
Metadata
Title: The Mathematical Building Blocks of Neural Networks
Number: 2
Book: Chollet: Deep Learning
Core Ideas
The chapter starts with a walkthrough of a motivational example in Keras, training a classifier to recognize the mnist handwritten digits.
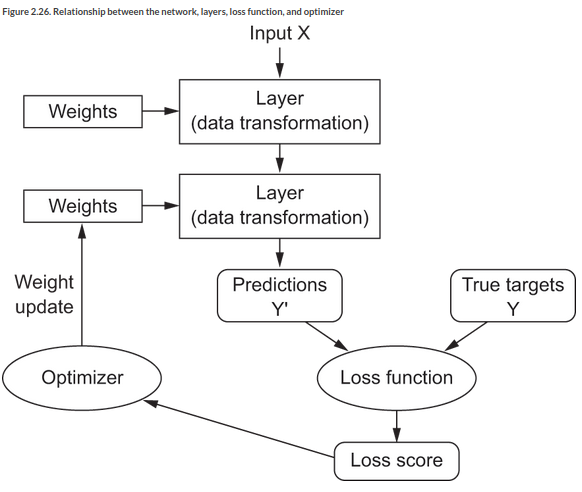
It introduces the main components of a deep learning model:
layers a filter for data, data goes in and comes out in a hopefully more useful form
optimizer the mechanism through which the model updates itself based on the data it sees, to improve its performance
loss function how the model will be able to measure its performance and steer itself in the right direction
metrics to monitor druing training and testing
Data Representation
All current machine learning systems use tensors as their basic data structures. So what’s a tensor?
At its core, a tensor is a container for data - usually numerical data. So, its a container for numbers… [T]ensors are a generalization of matrices to an arbitrary number of dimensions.
Note that in the context of tensors, dimensions are often called axes. We can classify tensors by their number of axes, also called the tensor’s rank.
You can display the number of axes in a NumPy tensor via the ndim attribute (x.ndim).
Scalars: Rank-0 tensors
A tensor that contains one number is a scalar, or 0D tensor, or rank-0 tensor. In NumPy a float32 or float64 number is a scalar tensor. Create one like this: x = np.array(12)
Vectors: Rank-1 tensors
An array of numbers is a vector or 1D tensor. It has exactly one axis. Create one like this: x = np.array([12,3,6,15,7]). This is a 5-dimensional vector (Not a 5D tensor!). A 5D vector has one axis, with 5 dimensions along its axis. Try to use tensor of rank 5 rather than 5D tensor to avoid ambiguity.
Matrices: Rank-2 tensors
An array of vectors is a matrix or rank-2 tensor/2D tensor. A matix has two axes, usually referred to its rows and columns. The entries from the first axis are rows, the second axis are columns.
Rank-3 and Higher
An array of matrices is a rank-3 tensor, an array of those is a rank-4 tensor and so on. In DL we generally manipulate tensors with ranks 0 to 4 (video may use 5).
main properties
We can explore the main properties of a tensor as follows:
# rank
x.ndim
# shape
# a tuple of integers with the dimensions the tensor has on each axis
x.shape
# a scalar will have an empty shape
# a vector will have a single element eg (5,)
# a matrix will have shape (r,c)
# data type
# the type of data contained in the tensor
# eg float16, float32, uint8
x.dtype
The first axis on any data tensor will be the sample axis also called the samples dimension.
We also typically batch data for processing, so this first axis is also called the batch axis. You see this term used all the time.
Real World Tensors
Some examples of real world tensors are:
Vector Data
Rank -2 tensor of (samples, features). Each sample is a vector of numerical attributes. One of the most common cases. For example a dataset of text documents with each doc being a term frequence vector over a vocabulary.
Timeseries or Sequence Data
Rank-3 tensor of shape (samples, timesteps, features) where each sample is a sequence of length timesteps of feature vectors.
The time axis is always the second axis by convention. For example:
a Dataset of stock prices. Each minute we store the current price of the stock, highest price that minute, and lowest price that minute. Each day is then a matrix of
(390,3)and 250 days’ trading is(250,390,3).Tweets as a sequence of characters. Each tweet is a sequence of 280 characters from an alphabet of 128 unique characters. Then each character is a binary vector of 128 (all 0s except a 1 for the actual character), then each tweet is a matrix of
(180,128)
Images
Rank-4 tensor of shape (samples, height, width, channels) where each sample is a 2D grid of pixels, each pixel is a vector of values.
Videos
Rank-5 tensor of shape (samples, frames, height, width, channels)
Tensor Operations
The chapter then discusses the main Tensor Operations.
Geometric Intuition
The chapter develops some geometric interpretations of tensor operations.
For example adding vectors can be interpreted as geometric translation.
Rotation counter clockwise is dot product with a 2D matrix: [[cos(theta), -sin(theta)], [sin(theta), cos(theta)]].
Scaling is dot product with a 2D matrix: [[x_factor, 0], [0, y_factor]]
Linear transform is dot product with an arbitrary 2D matrix (includes rotation and scaling).
Affine transform is dot product with some matrix and addition by a vector. Note this is the \(y = W \cdot x + b\) computation of a dense layer. A dense layer without an activation function is an affine layer.
Note that Affine transforms are closed operations, if you apply them repeatedly you end up with an affine transform (so you could just have applied one affine transform in the first place). So a ‘deep’ network with just affine transforms would be a shallow network in disguise. This is why we need non-linear activation functions, like relu. With such activation functions, a chain of dense layers can implement very complex, non-linear transformations.
More generally, we can intuit deep learning on the geometric analogy of uncrumpling sheets of paper. Take some sheets and crumple them. That’s the input data. DL carefully uncrumples them by a sequence of simple steps to make them cleanly separable:
Uncrumpling paper balls is what machine learning is about: finding neat representations for complex, highly folded data manifolds in high-dimensional spaces (a manifold is a continuous surface, like our crumpled sheet of paper).
Gradient Based Optimization
The chapter then introduces the engine of machine learning, Gradient Based Optimization
Bringing It Together
We can start pulling this together now into an understanding of the overall picture of a Neural Network:
The chapter concludes by building up a simple model ‘from scratch’ using TF without much Keras. See pp 63-6 for this.