Static Embeddings (Jurafsky Martin)
As presented in Jurafsky Martin Chapter 06: Vector Semantics and Word Embeddings
In Vector Semantics JM introduce sparse word vector models with long dimensions corresponding to the vocabulary or documents in a collection.
An alternative approach, using short dense vectors, is known as embeddings. These vectors have a shorter number of dimensions, ranging from 50-1000. The dimensions lack a clear interpretation. They are dense, the values will be real-numbered, positive or negative, rather than the sparse vectors we’ve seen so far.
It turns out that using these dense vectors works better in every NLP task than sparse vectors. We don’t completely understand why, but intuitively our classifiers have to learn fewer weights, and are probably less prone to overfitting. They may also do a better job of capturing synonymy.
This section presents one of the leading examples of static embedding where the model learns one fixed embedding for every word in the vocabulary. This is in contrast to contextual embeddings like BERT where the vector for each word is different in different contexts.
The section focuses on skip-gram with negative sampling or SGNS. This algorithm is behind the popular word2vec package so is sometimes informally called that.
The intution behind word2vec is that instead of counting how often context word w occurs near a given target word, we train a classifier on a binary prediction: “is context word c likely to show up near the target word?” We don’t care about the prediction task itself, we’ll take the learned weights as the word embeddings.
The revolutionary idea was that we can use running text as implicitly supervised training data for that classifier. A word c that occurs near the target word acts as a gold correct answer to the question “is word c likely to show up near the target word?". This method is called self-supervision and avoids the need for hand-labeled supervision signals.
This method was pioneered for neural language modeling. The word2vec model is simpler, it focuses on binary classification rather than predicting the next word, and it simplifies the architecture by using Logistic Regression rather than a multi-layer neural network. In skip-gram we:
Treat the target word and a neighbouring context word as positive examples.
Randomly sample other words in the lexicon to get negative samples.
Use logistic regression to train a classifier to distinguish between those two cases.
Use the learned weights as the embeddings.
Classification
We start by understanding the classification task. Take a target word apricot, a window of +/- two words, and a sentence like: “… lemon, a [tablespoon (c1) of (c2) apricot (w) jam (c3), a (c4)] pinch…". Our goal is to train a classifier that when given a tuple (w,c) of a target word w and a candidate context word c returns the probability that c is a real context word: \(P( + | w,c)\).
How does the classifier compute P? In skip-gram the probability is based on the similarity of the embeddings. A word is likely to occur near the target if it has similar embedding vectors. We rely on the intuition that the vectors are similar if their dot product is high (remember cosine is just a normalized dot product). The dot product can range from \([-\infty, +\infty]\), so to turn it into a probability we have to use the logistic or sigmoid function \(\sigma (x)\) as discussed in Logistic Regression:
\[\sigma(x) = \frac{1}{1+ \exp (-x)}\]
Then we can model the probability that c is a real context word for w as:
\[P(+|w,c) = \sigma(\mathbf{c} \cdot \mathbf{w}) = \frac{1}{1 + \exp (-\mathbf{c} \cdot \mathbf{w})}\]
We can then estimate that the probabilty of c not being a real context word is \(1 - P(+|w,c)\) to get a probability. This is just the probability for one word, but there are many context words in the window. Skip-gram assumes their probabilities are independent so we can multiply them:
\[P(+|w,c_{1:L}) = \prod^L_{i=1} \sigma (\mathbf{c_i} \cdot \mathbf{w})\]
\[\log P(+|w,c_{1:L}) = \sum^L_{i=1} \log \sigma (\mathbf{c_i} \cdot \mathbf{w})\]
In summary, skip-gram trains a probabilistic classifier that, given a test target word w and its context window of L words \(c_{1:L}\), assigns a probability based on how similar this context window is to the target word. The probability is based on applying the logistic (sigmoid) function to the dot product of the embeddings of the target word with each context word. To compute this probability, we just need embeddings for each target word and context word in the vocabulary.
Skip-gram stores two embeddings for each word, one for the word as a target, one for the word as context. The parameters to learn are two matrices W and C, each containing an embedding for every one of the |V| words in the vocabulary V. This is summarized as:

Learning the Embeddings
We now turn to how skip-gram learns the embeddings to use in the classification. It takes as input a corpus of text, and a chosen vocabulary size N. It begins by assigning a random vector for each of the N vocabulary words, and then iteratively shifts the embeddings for each word w to be more like the embeddings of words that occur nearby, and less like the embeddings that don’t. If we start with the apricot example above we have a target word w and 4 context words in the window, creating four positive training instances.
We also need negative exmaples, for each of these training instances we create k negative samples which are the target word and a noise word, which is a random word from the lexicon, not the target word. Noise words are chosen according to their weighted unigram frequency where the weight is often set to 0.75. This gives rare noise words slightly higher probability.
Given the set of positive and negative training instances, and a set of embeddings, the goal of the learning algorithm is to adjust the embeddings to:
Maximize the similarity of the target word, context word pairs \((w,c_{pos})\) drawn from the positive examples.
Minimize the similarity of the \((w,c_{neg})\) pairs from the negative examples.
We want to maximize the dot product of the word with the actual context words, and minimize the dot products of the word with the k negative sampled non-neighbour words. We can formalize this in a loss function:
\[L_{CE} = - \log \left[ P(+|w,c_{pos}) \prod^k_{i=1} P(- | w, c_{neg_i}) \right]\]
\[= - \left[ \log P(+|w,c_{pos}) + \sum^k_{i=1} \log P(- | w, c_{neg_i}) \right]\]
\[= - \left[ \log P(+|w,c_{pos}) + \sum^k_{i=1} \log (1 - P( + | w, c_{neg_i})) \right]\]
\[= - \left[ \log \sigma (c_{pos} \cdot w) + \sum^k_{i=1} \log \sigma (-c_{neg_i} \cdot w) \right]\]
We can minimize this through Stochastic Gradient Descent. The chapter has the gradients and the formula for updating the embeddings at each step.
The skip-gram model learns two separate embeddings for each word, the target embedding and the context embedding, stored in two matrices, the target matrix and the context matrix. It’s common to add the two vectors together, or just throw away the context matrix altogether.
The window size will affect the performance of skip-gram embeddings, and experiments often fine tune the paramater L (window size) on a devset.
Note that there is inherent variability, given the randomness in the initialization and the random negative sampling. So it is often best practice to train multiple embeddings with bootstrap sampling and average the results.
Alternative Embeddings
fasttext is an extension of word2vec that deals with a couple of issues in the original: namely unknown words in the test set, and word sparsity (eg in languages with a rich morphology).
Fasttext uses subword models to deal with these issues, representing each word as itself and a bag of constituent n-grams, with the boundary symbols ‘<’ and ‘>’ added to each word. For example if n = 3 then the word where would be represented as:
[‘
A skipgram embedding is then learned for each constituent n-gram, and the word where is represented by the sum of the embeddings of its constituent n-grams. Unknown words can be represented only by the sum of their constituent n-grams. Check out http://fasttext.cc for a library and pre-trained embeddings.
Another widely used model is GloVe, short for Global Vectors, and based on ratios of probabilities from the word-word co-occurrence matrix.
Dense embeddings have an elegant mathematical relationship with sparse embeddings like PPMI, in which they implicitly optimize a shifted PPMI matrix.
Semantics of Embeddings
Different types of similarity
It’s helpful to distinguish two kinds of similarity or association between words. Two words have first-order co-occurrence if they are typically near each other (eg wrote is a first-order associate of book, letter, poem). Words have second-order co-occurrence if they have similar neighbours (eg wrote is a second-order associate of said and remarked).
One critical choice in any vector semantic model is the size of the context window. Shorter context windows lead to representations that are more syntactic. When the window is short, words similar to a target word will be semantically similar words with the same parts of speech. When the windows are longer, the highest similarity scores will be words that are topically related but not similar. Eg Levy and Goldberg paper shows that with a window of +/- 2 Hogwarts was most closely related to other fictional schools. While with +/- 5 it was most closely related to other terms in Harry Potter, like Dumbledore, Malfoy etc.
Analogical Similarity
Embeddings can capture relational meanings. In the 1970s a parallelogram model was proposed for solving simple analogy problems like a is to b as a’ is to…? This model got new attention recently with dense embeddings as it seemd to capture relations like ‘male-female’ and ‘capital city of’, or ‘comparative-superlative’. as ‘king’ - ‘man’ + ‘woman’ gives a vector close to queen.
There are caveats though, it only seems to work well with frequent words, small distances, and certain relations. We also have to explicitly exclude variants of the input words. It’s argued that the model is just too simple to really model analogies very well.
Historical Semantics
Embeddings can be useful for showing how meanings change over time. By computing multiple embedding spaces, each from texts written in a particular period. For example:
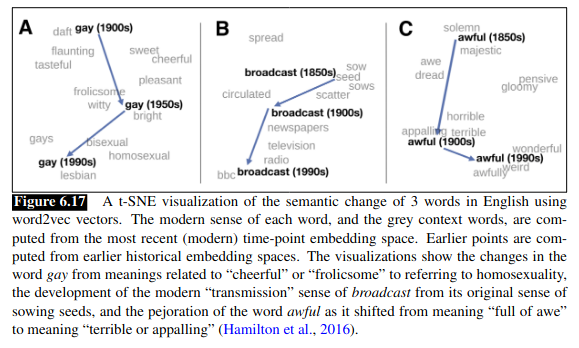
Bias and Embeddings
Embeddings reproduce, and amplify, biases and stereotypes that are latent in their source corpora. The chapter summarizes and reference lots of research on this. Examples include gender stereotypes where using the parallelogram method shows ‘father’ is to ‘doctor’ as ‘mother’ is to ‘nurse’ for example. This risks allocational harm if systems are built on top of such latent gender bias to, for example, recruit for positions.
Embeddings also exhibit stereotyped implicit associations that replicate, for example, racial stereotyping found in people. Eg African American names had a higher GloVe cosine with unpleasant words while European-American names had a higher cosine with pleasant words. Any embedding-aware algorithm that makes use of sentiment might bias against African Americans accordingly. This is an example of representational harm.
It remains an open problem of how to debias such embedding models. It is also possible to investigate historical biases and stereotypes through embedding models.