Generalization in Deep Learning (Chollet)
As presented in Chollet: Chapter O5: Fundamentals of Machine Learning Section I.
Overfitting and Underfitting
There is a universal pattern where performance on held-out validation data improves as training goes on until a point, then peaks (shows the same graph of this as cm3015 Topic 04: Model Improvement lectures). Frames it in terms of training time (epochs?) with Neural Nets rather than omdel complexity. Underfitting is not enough training in this context…
Overfitting is particularly likely to occur if data is noisy, if it includes rare features, or if it involves uncertainty.
Noisy Data
Real-world datasets will likely have invalid inputs, and valid inputs that have been mislabeled (even worse!). If a model adapts to incorporate these outliers, its generalization performance will degrade.
Uncertainty
Even clean and neatly labeled data can be noisy if the problem involves uncertainty and ambiguity. In classification, the same input feature space might be associated with multiple classes due to elements of subjectivity in the boundaries between them. Similarly many problems involve a degree of randomness, like predicting rain baed on atmospheric pressure.
A model can overfit to such noisy or probabilistic data by being too confident about ambiguous regions of the feature space. A more robust fit ignores individual data points and looks at the bigger picture:

Rare Features and Spurious Correlations
ML models trained on datasets that include rare features are highly susceptible to overfitting. In sentiment classification, if a rare word occurs in only one text, that happens to be negative sentiment, poor regularization will mean that this word has a high negative weight in the model.
Even if it’s not that rare, if there’s a statistical fluke in the distribution (say a word occurs 100 times and 54% of the time it’s positive by chance), the model will leverage that feature. This is one of the most common sources of overfitting.
In cases where you aren’t sure whether the features you have are informative or distracting, it’s common to do feature selection, eg the top 10,000 words. A common way of doing this is to compute some usefulness score with respect to the task, like mutual information between feature and labels, and only keep features above a threshold. This helps filter out noise.
Deep learning models can fit anything if they have enough representational power. You could generate white noise and train a model to fit it. So how come deep learning models generalize at all? Don’t they just learn an ad-hoc, arbitrary mapping? Why should we expect them to predict new data successfully?
This has nothing to do with DL models themselves, but the structure of information in the real world.
The Manifold Hypothesis
Take the handwritten character example. We have a 28x28 array of integers between 0 and 255. The number of possible inputs is \(256^784\) - greater than the number of atoms in the universe. But the actual handwritten digits are a tiny subspace of this parent space, and it’s highly structured, not random.
The subspace is continuous, if you take a sample and modify it a bit it will still be recognizable as the same digit.
All samples in the valid subspace are connected by smooth paths that run through it. If you take two different random digits, there exists a sequence of “intermediate” images that morph one to the other, such that two consecutive digits are very close to each other. Even the ambiguous shapes close to the boundary will look digit-like.
You can say that the handwritten digits form a manifold within the space of possible 28 x 28 integer arrays.
A manifold is a lower-dimensional subspace of some parent space that is locally similar to a linear (Euclidean) space. For instance, a smooth curve in the plane is a 1D manifold within a 2D space, because for every point of the curve, you can draw a tangent (the curve can be approximated by a line at every point). A smooth surface within a 3D space is a 2D manifold.
More generally, the manifold hypothesis posits that all natural data lies on a lower-dimensional manifold within the high-dimensional space where it is encoded.
This is even true of natural language, as it is for the sound of a voice, human faces, tree morphology etc. It’s a very bold claim, but seems to be true. And it enables DL to work.
The implications of the manifold hypothesis are:
ML models only have to fit relatively simple, low-dimensional, highly structured subspaces within their potential input space (latent manifolds).
Within one of these manifolds, it’s always possible to interpolate between two inputs, ie morph one into another via a continuous path along which all points fall on the manifold.
The ability to interpolate between samples is the key to understanding generalization in deep learning.
Interpolation
If you work with data that can be interpolated, you can start making sense of points you’ve never seen before by relating them to other points that lie close to the manifold. You can make sense of the totality of the space using only a sample of it. Interpolation fills in the blanks.
Interpolation on the linear manifold is different from linear interpolation in the parent space. Every point on the latent manifold is a valid digit. Manifold interpolation is an intermediate point on the manifold (a valid digit). Linear interpolation or average in the encoding space, usually is not a valid digit.
DL achieves generalization by interpolation on a learned approximation of the data manifold. But that’s not all there is to generalization. Interpolation enables local generalization, making sense of things that are close to what you’ve seen before. Humans are capable of extreme generalization, dealing with situations of extreme novelty without learning and rehearsal. This is enabled by other cognitive mechanisms, abstraction, symbolic modeling, reasoning, logic, common sense, innate priors. Not just intuition and pattern recognition.
Training Data
The power to generalize is a consequence of the structure of the data, not a property of the model. You’ll only be able to generalize if your data forms a manifold where points can be interpolated. The more informative and less noisy your features, the better you will be able to generalize.
Data curation and feature engineering are essential to generalization. … Further, because deep learning is curve fitting, for a model to perform well it needs to be trained on a dense sampling of its input space. A “dense sampling” in this context means that the training data should densely cover the entirety of the input data manifold. This is especially true near decision boundaries.
If sampling is sufficiently dense, it becomes possible to interpolate between training inputs without using common sense, abstract reasoning, and external knowledge.
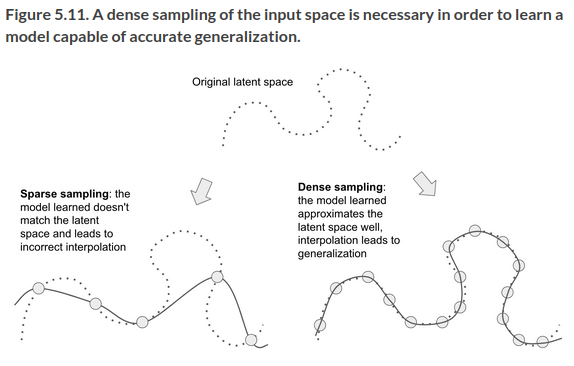
Denser coverage of the input data manifold will yield a model that generalizes better.
You should never expect a deep learning model to perform anything more than crude interpolation between its training samples, and thus you should do everything you can to make interpolation as easy as possible. The only thing you will find in a deep learning model is what you put into it: the priors encoded in its architecture and the data it was trained on.
If you can’t get more data, the next best thing is modulating the quantity of information your model is allowed to store, or add constraints on the smoothness of its curve. If a network can only afford to memorize a small number of patterns, the optimization process will force it to focus on the most prominent ones, and stand a better chance of generalizing. This is called regularization, covered in a separate section/note.