Evaluating Machine Learning Models (Chollet)
As set out in Chollet: Chapter O5: Fundamentals of Machine Learning, section 2.
It’s essential to be able to reliably measure the generalization power of your model.
Training, Validation, and Test Sets
Evaluating a model always boils down to splitting the available data into three sets: training, validation, and test. You train on the training set, evaluate on the validation set. When ready for prime time you do one final test on the test data. Then you deploy.
Why three sets rather than two? Because we need to tune the model configuration, its hyperparameters (eg the number and size of the layers of a network). You tune by using performance on the validation set as a feedback signal. So the tuning is a form of learning itself - search for a good configuration in the hyperparameter space. So tuning on the validation set can lead to overfitting on that set.
This is captured in the concept of an information leak, every time you tune your hyperparameter on the validation set, some information about it leaks into the model. If you do this many times, you’ll leak an increasingly significant amount of information.
You need to evaluate it on a set that the model has had no sight of before evaluation. There are several common methods for doing this three-way split.
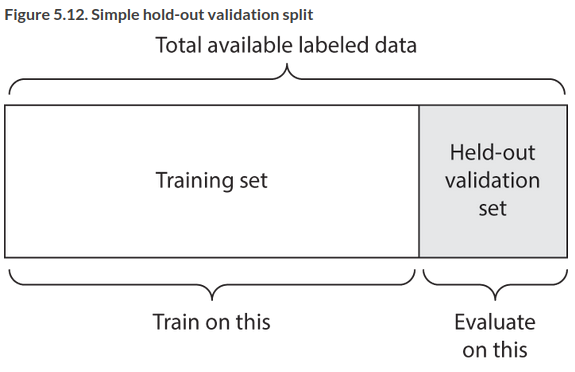
Simple Holdout Validation
Set apart a fraction of your data for testing, train on the rest. You shouldn’t tune on the test set so you also need to reserve a validation set.
This is the simplest protocol, suffering from one flaw: if little data is available then your validation and test sets may contain too few samples to be statistically representative of the data at hand. You can spot this easily. If random shuffling rounds of the data before splitting yields very different model performance, you have this issue.
K-fold Validation
Split your data into K partitions of equal size. For each partition i train a model on the remaining K-1 partitions, and evaluate it on partition i. Your final score is the average of the K scores obtained. Helpful wehen the performance shows significant variance based on how you do the train/test split. You still need to reserve a validation set.

Iterated K-fold validation with shuffling
Use this if you have relatively little data available, and need to evaluate the model as precisely as possible (Chollet uses it in Kaggle competitions).
You apply K-fold validation multiple times, shuffling the data every time before splitting it K ways. The final score is the average of the scores obtained at each run. It’s expensive as you end up training and evaluating \(P \times K\) models where P is the number of iterations.
Performance Baselines
Training a DL model happens in a space with thousands of dimensions. You can’t see it. If you project it down to 3D you couldn’t interpet it. The only feedback you have is validation metrics.
How do you know if you’re getting off the ground? Your model has an accuracy of /x/%, is that any good? You need to set a baseline that you’re trying to beat. The baseline could be the performance of a random classifier. Or the simplest non ML technique you could think of.
For instance, if you have a binary classification where 90% of the samples are in one class, you should try to beat 0.9. In an even distribution you’d need to beat 0.5
This is especially important in problems that haven’t been solved before. If you can’t beat a trivial solution your model is worthless.
Pointers on Model Evaluation
Make sure both your training and test sets are representative. You should usually randomly shuffle your data before splitting it. It’s surprisingly common to make a silly mistake like sorting your data by class and then splitting, so you only take the first 80% for training and don’t train on 20% of your classes, but test exclusively on those…
If your data is temporal then don’t shuffle it! If you’re predicting the future based on the past, you need to avoid temporal leaks and make sure your test set is posterior to your training set.
Make sure your training and test sets are disjoint. It’s common in real world data sets for data to occur twice. If you randomly shuffle and split you could end up testing on your training data.