Gradient Based Optimization (Chollet)

When we transform our data in a NN layer with a function like relu(dot(input, W) + b) The matrix W and vector b are weights or parameters of the layer. Specifically the W matrix is known as the kernel attribute, and the b vector is known as the bias attribute.

Initially these are filled with small random values (initialization), and then we try to improve them. The gradual improvement is called training, and takes place in the training loop:

1. Draw a batch of training samples, x, and targets, y_true.

2. Run the model on x (called the forward pass) to obtain predictions y_pred.

3. Compute the loss of the model on the batch, ie measure the mismatch between y_true and y_pred.

4. Update all the weights of the model in a way that slightly reduces the loss on the batch.

Step 1 is straightforward I/O. Steps 2 and 3 are just applying the simple Tensor Operations. But step 4 is the hard bit. How do we update the weights? Should we increase or decrease a particular coefficient. How much?

A naive approach would be to just freeze all weights but one, then re-do the forward pass with a higher or lower value. No way this can scale to the 1000s or millions of individual coefficients in a large model. Instead we use gradient descent.

The essential gist is that all of the functions used in the layers are continuous, transforming their input in a smooth way. This means they are differentiable. If you chain the functions together, the bigger function is still continuous, and differentiable.

Crucially, this applies equally to the function that maps the model coefficients to its loss value. A small change to the coefficients will produce a small, predictable change in the loss. So you can you can use the gradient operation to describe how the loss varies as we move the coefficients. We move them against the gradient, and so decrease the loss.

The chapter then introduces the derivative as the function mapping x to the slope of the local linear approximation of f.

Derivative of a Tensor

You’re used to derivatives of functions that take a scalar x to a scalar y - they can be plotted as a curve in 2D.

But you could also have a function that maps a tuple of scalars (x,y) to a third scalar z. Here we’d plot this as a 2D surface in 3 dimensions. This can be extended to higher rank tensors.

We can still apply the concept of derivation to such a function, so long as they surfaces they describe are continuous and smooth.

The derivative of a tensor operation (or tensor function) is called a gradient. Gradients are just the generalization of the concept of derivatives to functions that take tensors as inputs… the gradient of a tensor function represents the curvature of the multidimensional surface described by the function. It characterizes how the output of the function varies when its input parameters vary.

Putting it programmatically, we can take the loss value to be a function of the current model weights, f(W). Then the derivative of f at the point W0 is a tensor grad(loss_value, W0), with the same shape as W, where each coefficient indicates the direction and magnitude of the change in loss value you would see when modifying the equivalent weight coefficient.

So we can update our parameters and take the next step by moving against the gradient, decreasing the loss: W1 = W0 - step * grad(f(W0), W0). Note we have to multiply by a scalar to avoid moving too far from W0.

Stochastic Gradient Descent

It’s possible to calculate analytically where the derivative is 0 (so local/global max/min), but in practice it’s intractable for large neural nets. So we follow the algorithm:

Draw a batch of training samples and corresponding targets.

Run the model to obtain its predictions (the forward pass)

Compute the loss

Compute the gradient of the loss (the backward pass)

Move the parameters a little in the opposite direction of the gradient.

This is mini-batch stochastic gradient descent. Stochastic here means random, and refers to the fact that the mini-batch is drawn at random. Alternatives are batch gradient descent where we run the whole dataset through each time (too expensive), or true SGD where we draw a random single sample (too erratic).

There are more variations too, for example some take account of previous weight updates, not just the current gradient value. These variations are known as optimizers. One intuitive concept in some of these optimizers is momentum. To avoid getting stuck in local minima, the algorithm may maintain some momentum up the opposite slope to see if it can resume a downhill trajectory after an initial rise (like a ball rolling in physics).

Backpropagation

So how do we compute the gradient of a differentiable function? How do we do it when we have multiple layers, which might produce a complex expression from the simple atomic Tensor operations. This is the role of the backpropagation algorithm.

With backpropagation we can use the derivatives of simple operations to compute the gradient of arbitrarily complex operations. It relies on the chain rule from calculus. Consider a set of functions f, g, h, j such that their compound fghj(x) == f(g(h(j(x)))). Then the chain rule works like this:

def fghj(x):
    x1 = j(x)
    x2 = h(x1)
    x3 = g(x2)
    y = f(x3)
    return y

grad(y,x) == (grad(y, x3) * grad(x3,x2) *
	      grad(x2, x1) * grad(x1,x))

So long as we know the derivatives of the intermediate steps then, we can compute the overall gradient. Applying the chain rule to the gradient values of a NN produces the backpropagation algorithm.

A computation graph is the data structure at the heart of Tensor Flow and understanding backpropagation. It is a directed, acyclic graph of operations (in the case of TF, tensor operations). They allow us to treat computation as data. A computable expression is encoded as a machine readable data structure that can be used as input or output to other programs. For example a program could take a computation graph as input and produce a distributed version of that computation as output, for scaling. Or a program could take a computation and produce its derivative.

Here’s a simple graph, see pages 58-9 in the book for a full worked example in diagrams:

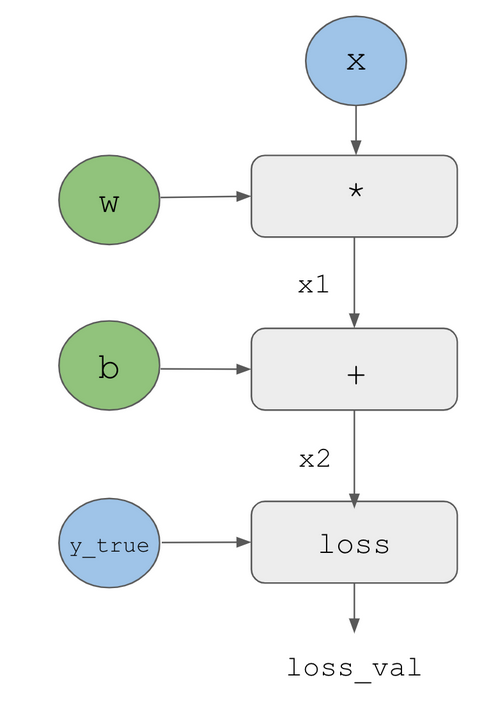
To get the gradients we can first do a forward pass propagating the graph with concrete values from top to bottom.

Then we can create an opposite edge and ask how much does B vary when A varies. This is the backward pass.

Finally we can apply the chain rule to multiply the derivatives for each edge along the path to get the overall gradient.

And that’s it! Backpropagation is just the application of the chain rule to a computation graph. We “back propagate” the loss contributions of different nodes in a computation graph. Nowadays we use frameworks like TF that are capable of automatic differentiation based on the computation graph, so we don’t have to calculate all the derivatives by hand.

The TensorFlow Gradient Tape

The TF GradientTape gives an API to access the automatic differentiation capability. It creates a scope that records the tensor operations run inside it, in the form of a computation graph, or tape. The graph can then be used to retrieve the gradient of any output with respect to any variable or set of variables (tf.Variable instances - a class meant to hold mutable state). The weights of a NN are always tf.Variable instances.

A quick example, there is more in ch. 3:

x = tf.Variable(tf.random.uniform((2,2))

with tf.GradientTape() as tape:
    y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y,x)