Convolutional Neural Networks
As presented in Chollet: Chapter O8: Intro to DL for Computer Vision
To get an overall sense of a CNN/convnet take a look at this example for the MNIST dataset:
from tensorflow import keras
from tensorflow.keras import layers
inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
model.summary()
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 28, 28, 1)] 0
_________________________________________________________________
conv2d (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 13, 13, 32) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 11, 11, 64) 18496
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 3, 3, 128) 73856
_________________________________________________________________
flatten (Flatten) (None, 1152) 0
_________________________________________________________________
dense (Dense) (None, 10) 11530
=================================================================
Total params: 104,202
Trainable params: 104,202
Non-trainable params: 0
_________________________________________________________________
A convnet takes input tensors of shape (img_height, img_width, img_channels)
Note the output of every Conv2D and MaxPooling2D layer is a rank-3 tensor of shape (height, width, channels), with the width and height shrinking as you go deeper in the model. You control the no. of channels with the filters parameter.
If you train this network on MNIST you’ll see it does much better than a densely connected model. How come?
The Convolution Operation
The visual world forms a spatial hierarchy of visual modules. Elementary lines or textures combine into simple objects, such as eyes or ears, which combine into high-level concepts like cat. CNNs can learn spatial hierarchies of patterns.
Unlike Dense layers, which learn global patterns in their input feature space, a convolution layer learns local patterns. In images, these are patterns found in small 2D windows of the input.
These patterns are translation invariant. After learning a pattern in the lower-right corner of an input image, a convnet can recognize it anywhere, eg in the upper-left. Whereas a dense layer would have to learn that as a whole new pattern. This matters because the visual world is fundamentally translation invariant.
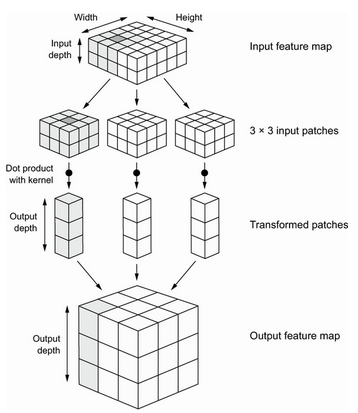
We’re used to thinking of images as represented in rank-3 tensors of shape (width, height, channels). The channels (or depth) of the image would represent RGB or greyscale, for example. In convolution operations these tensors are called feature maps
The convolution operation extracts patches from its input feature map and applies the same transformation to all of these patches, producing an output feature map. This output feature map is still a rank-3 tensor: it has a width and a height. Its depth can be be arbitrary, because the output depth is a parameter of the layer, and the different channeels in that depth axis no longer stand for specific colors as in RGB input; rather, they stand for filters. Filters encode specific aspects of the input data: at a high level, a single filter could encode the concept “presense of a face in the data” for instance.
In the example, the first convolutional layer took a feature map of size (28, 28, 1) and output a feature map of (26, 26, 32), ie it computed 32 filters over its input. Each of those 32 output channels is itself a 26 x 26 grid of values, which is a response map of the filter over the initial input.
So every dimension in the depth axis of the feature map is a feature or filter. The rank-2 tensor [:,:,n] is the 2D spatial map of the response of this filter over the input. Hence feature map.
This means there are two key parameters in defining a convolution layer: the size of the patches extracted, typically 3x3; and the depth of the feature map, the example started with a depth of 32, and ended with a depth of 64.
The convolution operation works by sliding the 3x3 window (or 5x5 etc) over the 3D input feature map, stopping at each location and extracting the 3D patch of surrounding features (shape (window_height, window_width, input_depth)). The 3D patch is transformed into a 1D vector of shape (output_depth,) via a tensor product with the weight matrix, called the convolution kernel.
The resulting vectors (one per patch) are then re-assembled into a 3D output map of shape (height, width, output_depth), where every spatial location corresponds to the same location in the input feature map.
The output width and height may differ from the input due to border effects (unless you pad the input, see the padding argument), and strides.
The distance between two successive windows is its stride, which defaults to 1. Using a stride of 2, for example, will downsample the input by a factor of 2. This is rare in classification, but used elsewhere. In classification we downsample with the max-pooling operation instead.
Max-Pooling
In the example above notice that the output of the MaxPooling2D layers halves the size of the feature maps. It aggressively downsamples the feature map, like using stride.
It works by extracting windows from the input feature maps and outputting the maximum value of each channel. It’s similar to convolution, except instead of learning a linear transformation, it applies a hardcoded max tensor operation.
Max pooling is usually done with 2 x 2 windows and stride 2, to downsample by a factor of 2. Convolution with 3 x 3 windows and stride 1 (ie no stride).
Why bother to do this? Imagine the same network with no max-pooling layers. The issue is that it’s hard to then learn spatial hierarchies. Each 3x3 window in the third convolution layer corresponds to a 7x7 grid in the original. These are still small patterns, how would you classify a digit only looking at it in windows of 7x7 pixels?! We need the last layer to encode information about the whole input.
The other issue would be overfitting. Pushing a final convolution layer into a dense softmax classifier of eg size 10 would produce over half a million parameters. That’s too big for a small model.
You can use average pooling instead of max pooling, but max pooling works better.
The most reasonable subsampling strategy is to first produce dense maps of features (via unstrided convolutions) and then look at the maximal activation of the features over small patches, rather than looking at sparser windows of the inputs (via strided convolutions) or averaging input patches, which could cause you to miss or dilute feature-presence information.
Preprocessing Image Data
Preparing a set of image files for convnets can be fairly involved, you have to read the picture file, decode the file format and create a RGB grid of pixels, convert them to floating point tensors of the right scale, resize them to a common size, and batch them.
Keras offers a utility function to do all that for you, called image_dataset_from_directory it’s in tensorflow.keras.utils.
It lists the subdirectories and assumes each one contains images from a calss. It will index the image files, create and return a tf.data.Dataset object configured to read the files, shuffle them, decode them to tensors, resize them, and pack them into batches.
See p. 217 of the book for a worked example.
For rescaling, Keras offers a Rescaling layer where you can pass the rescaling operation to do (eg 1./255 to convert standard RGB to the [0,1] range.