Chollet: Chapter 10: Deep Learning for Timeseries
Metadata
Title: Deep Learning for Timeseries
Number: 10
Core Ideas
A timeseries can be any data obtained by measurements at regular intervals, like daily stock price, hourly electricity consumption, or weekly sales. They can be natural phenomena (weather), or human activity patterns (web usage stats, credit card transactions).
Working with timeseries involves understanding the dynamics of a system, periodic cycles, trends over time, the regular regime and sudden spikes.
By far the most common timeseries-related task is forecasting, predicting what will happen next in a series. Forecast electricity consumption, forecast product demand, forecast revenue, forecast the weather etc. That’s the focus of the chapter too, but there are other tasks related to timeseries:
Classification - Assign one or more categorical variables to a timeseries. EG given a website visitor, classify as bot or human.
Event detection - Identify the occurence of a specified expected event within a continuous data stream. Eg detect an utterance like ‘Hey Alexa’ while monitoring an audio stream.
Anomaly detection - Detect anything unusual happening within a continuous datastream. Unusual activity in your network, unusual readings in a manufacturing line. This is often done via unsupervised learning.
A distinctive feature of timeseries data is domain specific representation techniques. EG fourier transforms for preprocessing any data that is characterized by cycles and oscillations. Such feature engineering is common for timeseries. But the chapter focuses on the network modelling, especially recurrent neural networks.
The chapter starts by setting up an example, involving temperature forecasting. Pages 284-7 look at inspecting and preparing timeseries data for DL. Key points include always to look for periodicity in your data. It also walks through the
timeseries_dataset_from_arrayutility in keras.It then looks at establishing baselines for timeseries forecasting (p. 288). Given the variable is often continuous, a baseline might be just predict for the next timestep what you saw in the previous one. This can often be hard to beat!
It then looks at why simple dense layers don’t work. We know there’s a simple mapping from data to prediction, why can’t we find it? The issue is that the search space of possible models in, eg, a 2 layer NN is very large. Just because there is a common-sense heuristic doesn’t mean you’ll find it with gradient descent. This is an issue with ML in general, and why feature engineering and thinking through your architecture’s priors is so essential. Otherwise you’re looking fairly blindly for a needle in a haystack.
1D Convolutions
We encountered 2D convolutions in image data, but there are also 1D and 3D convolutions that work on the same principle. A Conv1D layer relies on 1D windows that slide across input sequences.
1D convolutions are a great fit for any sequence data that follows the translation invariance assumption (meaning that if you slide a window over the sequence, the content of the window should follow the same properties independently of the location of the window).
In the case of the temperature forecasting example, though, it performs even worse than a dense layer stack. Why?
Weather data doesn’t respect the translation invariance assumption. While the data features daily cycles, data from the morning follows different properties than data from the evening or middle of the night. Weather data is only translation invariant for a specific timescale.
Order in our data matters, a lot. The recent past is way more informative than data from five days ago. A 1D convnet can’t leverage this. In fact combined with max pooling you may well destroy that information.
So dense layers flatten the notion of time, and convolutions treat all segments the same, destroying the importance of order. There has to be a better way, Jim!
Recurrent Neural Networks
There is! The answer is Recurrent Neural Networks.
Advanced Use of RNNs
The chapter then discusses three more techniques with RNNs:
Recurrent Dropout
RNNs often overfit quickly. Dropout is a standard technique to compensate, but how to apply dropout to RNNs is not easy. Applying dropout before a recurrent layer hinders rather than helps learning.
Essentially the same dropout mask has to be applied at every timestep, rather than using one that varies randomly between different layers. The temporally constant dropout mask should be applied to the inner recurrent activations of the layer itself too.
Doing it this way enables the network to propagate its learning error properly through time.
This is built into Keras (by the guy who discovered it for his PhD!), such that every recurrent layer in Keras has two dropout arguments. dropout, a float specifying the dropout rate for units of the layer, and recurrent_dropout, specifying the dropout rate of the recurrent units. See p. 301 for an example in action.
Stacking Recurrent Layers
Recurrent layer stacking is a classic way to build more powerful recurrent networks. Until recently Google Translate was powered by a stack of seven large LSTM layers (that’s very big).
You can keep adding layers until you start to see overfitting. You may reach a point of diminishing returns quickly, depending on the size of problem. See p. 303 for an example of stacking GRU layers.
Bidirectional RNNs
A bidirectional RNN is a common RNN variant that offers better performance on certain tasks. It’s especially common in NLP, it’s like the swiss army knife of DL NLP.
A bidirectional RNN exploits the order sensitivity of RNNs by using two regular RNNs (like GRU or LSTM) each of which processes the input sequence in one direction (the reverse of each other) and then merges their representations into one.
By processing the sequence in both ways, the bidirectional RNN can catch patterns that would be missed by just one direction.
In the case of natural language, the importance of a word in understanding a sentence isn’t usually dependent on its position in the sentence. You can read a sentence backwards just fine. Word order matters, but which order doesn’t.
A RNN trained on reverse sequences will learn different but useful representations. And in ML, different and useful is always worth exploring. This is the concept of ensembling which is widespread in the field.
A bidirectional RNN exploits this idea to look at the input sequence both ways and obtain potentially richer representations than just looking in one direction, here’s an illustration:
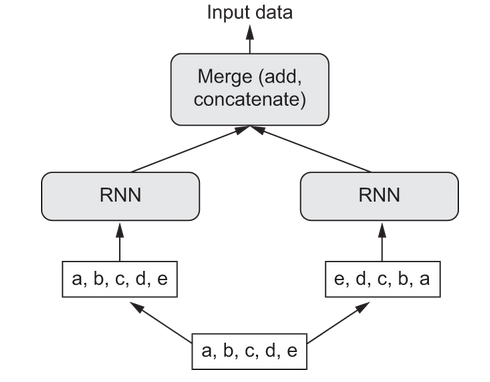
To create a bidirectional layer in keras you use Bidirectional which takes as its first argument a RNN layer instance. For example: x = layers.Bidirectional(layers.LSTM(16))
Until the emergence of Transformers, bidirectional RNNs were state of the art in NLP.