cm3020 Lecture Summaries: Topic 03: Reinforcement Learning
Lectures from the third case study in cm3020 Artificial Intelligence
Week One: Introduction
11.001: Introduction
Introduces the 2015 DeepMind DQN paper as the focus of the case study. Its main point of interest in his terms was that the agent only received images as input, and did the rest itself. He sees this as part of the trend to ‘generalized AI’ - agents learning to do tasks without detailed instructions.
Week 1 will introduce the history of game playing agents. Week 2 will formalise how an AI can learn a game. Week 3 will look at tooling, especially the Open AI gym and Convolutional Neural Networks. Week 4 will take the formalism and implement it in Python. Week 5 will review the state of the art, and ethics.
11.102: Overview of AI game playing
Gives a rambling overview of the field. We’re interested in games that humans play. “games are interesting because they are too hard to solve” (from Russell and Norvig: AI: A Modern Approach).
Mentions the ‘unfairness’ argument in Justesen et al: When are we done with games? - that competitions so far have been unfair against humans. We want to solve games because they will be useful step in solving real-world problems.g
Mentions the Grace et al: When Will AI Exceed Human Performance? Evidence from AI Experts paper on predictions for AI performance, experts over-estimated how long it would take for AI to outperform humans on Atari games.
Discusses commercial interests in AI game players. Computer game industry itself, of course. Discusses the Zhao et al: Winning isn’t everything paper that explains the limits of human playtesting.
Discusses the Togelius: The Mario AI Championship paper, and the role of competitions in evaluating algorithms. Competitions make it fair, provide motivation.
Presents the Moravec paradox: things humans find hard, not so difficult for AIs, things that humans find easy, AIs find hard. Gives a really weird example with the gist that generalization is challenging for computer agents.
Presents the Badia et al: Agent57: Outperforming the Atari Human Benchmark paper as the current state of the art.
Presents the Raiman et al: Long-Term Planning and Situational Awareness in OpenAI Five paper on the issue of long-term planning.
When we solve games? When you can go play it at any time (following Justesen et al: When are we done with games?).
11.104: Some Milestones
Gives a history of major milestones in game-playing AIs. Derived from Schaeffer: A Gamut of Games.
1950: Shannon: Programming a Computer to Play Chess one of the first formal descriptions of a chess playing algorithm.
1952: Strachey: Logical or non-mathematical programmes one of the first checker/drafts agents.
Skips some years, suggests we fill the blanks!
1979: Berliner: Backgammon computer program beats world champion
1989: Computer Olympiad, created by Daniel Levy, computer vs. computer competition.
1992: Schaeffer: A world championship caliber checkers program
1997: Campbell et al: Deep Blue. Custom hardware, massive search algorithm did huge crunching of chess moves.
2002: Sheppard: World-championship-caliber Scrabble
2007: Schaeffer: Checkers is Solved - AI plays the best possible game at every time.
2009: Togelius: The Mario AI Championship - 2009 the first competition (paper published later)
2015: Mnih et al: Human-level control through deep reinforcement learning - the DQN paper we’ll be studying.
2017: Silver et al: Mastering the Game of Go - recommends the Youtube video documentary
2018: Brown and Sandholm: Superhuman AI for heads-up no-limit poker
2019: Raiman et al: Long-Term Planning and Situational Awareness in OpenAI Five
2020: Badia et al: Agent57: Outperforming the Atari Human Benchmark
11.201: How might we build a game-playing AI?
Explains the choice of the DQN agent. There is a certain purity to it. Later versions bolt on lots of extra features that perform better but lose the clarity and simplicity of the original.
How do we write an AI player? Walks through a basic architecture - we’ll send the pixels from the screen to the agent, along with the score and whether it’s game over.
It outputs left, right, or nothing. The game updates. We can’t provide labels for every possible state.
Gives a definition of RL:
how agents can learn what to do in the absence of labeled examples of what to do… Imagine playing a new game whose rules you don’t know; after a hundred or so moves, your opponent announces, “you lose”. This is reinforcement learning in a nutshell. (Russell and Norvig)
Before we get to the formal model, we need to think about states, actions, and rewards.
States are the pixels coming in; actions are left, right, nothing; rewards are the score and game-over. This is what we need to formalize, and build algorithms to solve the problem.
Week Two: Formalisms
12.103 Formalising the Problem
Formalises the concepts of states, actions, and rewards:
The player observes state s.
The player takes action a.
The player observes the next state s’
\[s,a \rightarrow s’\]
This is stochastic, so we can add a probability P to the transition:
\[P(s’\; |\; a,s)\]
There is a reward associated with the \(s,a,s’\) construct: \(s,a,s’,r\) - taking an action a in state s leads to state s’ and a reward of r.
So the reward is a function on the \((s,a,s’)\) construct:
\[R(s,a,s’)\]
Combined these elements (the probablistic state transitions and the reward function) form a Markov decision process which is a way to formalise a stochastic sequential decision process.
12.105 Value Functions and DQN
Continues the formalisation of DL:
An action policy tells us what to do in a given state. Policies are denoted \(\pi\). So:
\[\pi(s) \rightarrow a\]
‘The policy for state s is to take action a’.
What would an optimal policy look like? This is a sequential problem, not one shot. Reward might come in the far future.
An optimal policy maximises reward over a sequence of actions. So the action you take now should unlock maximum potential rewards going into the future.
This can be formalised in the Bellman equation, which defines the value of a given action in a given state based on future reward:
\[V^*(s,a) = \max_\pi \sum \left[ r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \dots \;|\; s_t = s, a_t = a, \pi \right]\]
Where \(\gamma < 1\).
The value of action a in state s is the reward for s + max possible future reward for states s at time t, increasingly discounted by a factor gamma raised to the power of t.
This is simplified because it doesn’t included the state transitions.
We’re missing a state transition matrix, which tells us how the state will change over time based on our chosen actions.
We’re also missing the action policy which dictates what the chosen actions will be in each state. It involves choosing the highest value action.
But the complete transition matrix and associated rewards for Atari games is huge. So the perfect value function doesn’t help much on its own.
We need a way to approximate this perfect value function. That is what the Q-learning function provides. It approximates the value function. That approximation is the Q function.
This looks very much the same, except it’s a Q!
\[Q^*(s,a) = \max_\pi \sum \left[ r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \dots \;|\; s_t = s, a_t = a, \pi \right]\]
But on its own Q-learning doesn’t in practice work on real problems. It wasn’t until we approximated the Q function through deep learning that we started to get significant results. This was where the Deep Q Network or DQN contribution came in.
12.108 DQN Agent Architecture
An agent is an entity that can observe and act autonomously.
An agent architecture is the solution to the missing state transition matrix, and the missing action policy.
Shows the high level architecture:
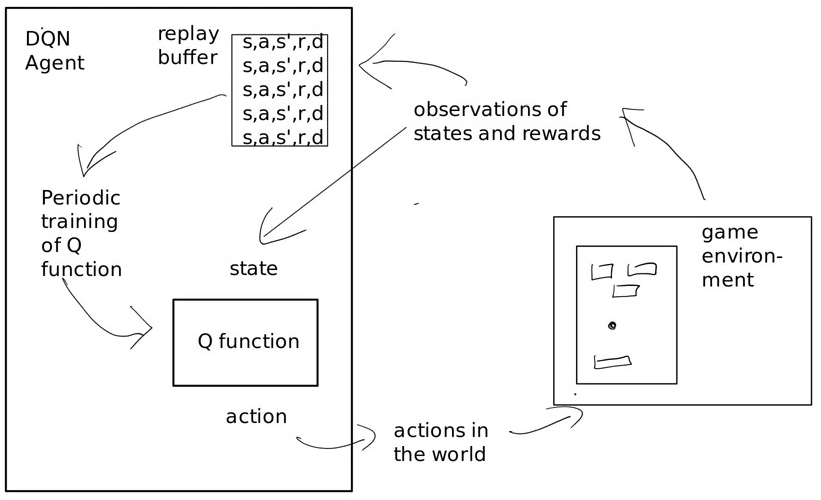
On the left you have the agent, on the right the task environment. The agent makes observations of the environment, its state and rewards.
The agent has a replay buffer, a record of the states, actions, successor state, and reward.
The other main component is the Q function
Training is periodic, after a set of observations it updates its Q function.
We generate the replay buffer by exploration, we explore the game and make observations of the form: \(s,a,s’,r,done\).
The method used to fill the buffer is epsilon greedy exploration. In the early days there is no Q function, it just takes a random action. The random actions are used to fill the buffer.
Epsilon is a value that changes over time, and determines the probability that you’ll choose an action based on the Q function rather than randomly.
Initially \(\epsilon\) is 0, so we purely act randomly. Then over time it grows so that we rely more on the Q function as we have more evidence in the buffer to go on.
12.110 The Loss Function for DQN
We need to train the Q function, ie the approximation of the value function for an action in a state.
We train it on the state transition data, the replay buffer. But remember that the Q function does not infer the next state, it infers the value of an action. We don’t have a ground truth for that.
Typically we have a labelled dataset for supervised training, that gives us the ground truth for assessing the current model’s loss and improving it via gradient descent.
So how do we assess loss when we don’t have a ground truth? By this loss function:
\[L_i (\Theta_i) = \sum_{s,a,r,s’} U(D) \left[ \left( r + \gamma \max_{a’} Q(s’,a’; \Theta_i^-) - Q(s,\;\Theta_i) \right) ^2 \right]\]
The proxy for the correct answer is the previous version of the network before we did this training. So we maintain two networks. A training network that we update all the time, and another that we update more slowly and use to evaluate the training one.
The \(\Theta\) refers to the model weights. So \(\Theta(_i)\) is the current model state. The loss of the current network then is everything on the right of =!
The expression \(\sum_{s,a,r,s’} U(D)\) says that we take a random sample of observations from the replay buffer (the \(U\) means uniform random sample, \(D\) the replay buffer), and will sum their losses.
The expression \(r + \gamma \max_{a’} Q(s’,a’; \Theta_i^-)\) is the approximation of what the model should return. Here \(\Theta_i^-\) is the prior model state. So we take the current known reward, and the predicted future reward based on the old model.
We compare that with the current estimate based on the current model and work out the difference. Over time the model will improve as the known signal (the actual reward) helps improve the information in the model.
12.112 Visual Processing and states in the DQN
Introduces the visual processing in DQN. The state is represented by three frames, which includes information about time and movement.
It gets a little more complex as you take the maximum value over two frames to produce one of these three frames. This is because the Atari only rendered some sprites on even frames, and others on odd frames.
So essentially we’re going from six ‘raw’ frames to three input frames that make up the state.
Then they strip the colour, they convert RGB to luminance, giving a single value per pixel.
Finally they rescale it to 84 x 84.
In total this strips out a lot of unneccessary information, while preserving the integrity of the image and adding sequence information.
Week Three: Tooling
The lectures introduce the Open AI gym and convnets with Keras.
Open AI Gym
A gym is a way of providing standardised environments for reinforcement learning algorithms to operate in. It allows the developer to focus on their agent rather than the simulation. It includes versioned, standard set of environments to enable comparison.
OpenAI Gym is summarised in Brockman: OpenAI Gym It aims to be accessible for developers to plug into using Python.
You can set up the gym with pip, the package name and import are both just gym. List avaiable environments with gym.envs.registry.all() (returns a dict values object).
Then we can set up an environment with something like: env = gym.make('LunarLanderContinuous-v2')
check out an environment’s action_space for what the actions are, step by calling env.step() with an action. You can sample() the action space for a random action.
Note that stepping returns some values. Specifically a tuple with (observation, reward, done, info).
So it provides the workflow for reinforcement learning - act, observe, reward.
13.201 Intro to Keras and NNs
Crash course on keras and neural networks. The input to the DQN NN is the game state, the output is the value of all actions. It learns the Q function.
Talks through units, layers, weights, activation and loss functions etc. All familiar from cm3015 Machine Learning and Neural Networks so not summarised again here.
13.203 Convolution Layers
Introduces Convolutional Neural Networks. The DQN uses convolutional nets.
Convolution is a filtering technique, often used for images, but also sound. You calculate the new value for a pixel by adding together scaled values of the original pixel and its surrounding pixels. It’s essentially a matrix multiplication. EG a blur operation would average out the pixel and its neighbours. Edge detection would emphasise different values and ignore similar ones [[-1,-1,-1],[-1,9,-1],[-1,-1,-1]].
A convnet applies trainable filters. We don’t hardcode filter values, we learn them by backpropagating the loss through the convnet filters.
The main properties of a convnet layer are the kernel size (usually 3x3, sometimes 5x5), the depth - how many filters are applied, and the stride, the hop size.
Includes a visualization of the convnet’s ‘view’ of the game as it plays. Taken from this repo
Week Four: Implementation
The lectures walk through the implementation of the DQN agent.
14.103 DQN Runtime
Gives an intro to the DQN agent runtime. Introduces the source of his implementation. It’s the most elegant. Also see the docs
Source is captured as a note: DQN Keras Implementation (Chapman and Lechner)
Shows a diagram of the runtime:
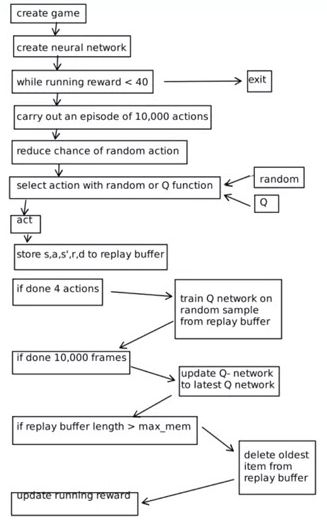
‘Running reward’ is the running score over the last few games.
The replay buffer in this implementation is just a series of lists, each containing the state, reward, next state, done results of the action.
14.105 DQN Network Architecture
Reviews the network architecture.
In Keras it looks like this from the DQN Keras Implementation (Chapman and Lechner):
def create_q_model():
# Network defined by the Deepmind paper
inputs = layers.Input(shape=(84, 84, 4,))
# Convolutions on the frames on the screen
layer1 = layers.Conv2D(32, 8, strides=4, activation="relu")(inputs)
layer2 = layers.Conv2D(64, 4, strides=2, activation="relu")(layer1)
layer3 = layers.Conv2D(64, 3, strides=1, activation="relu")(layer2)
layer4 = layers.Flatten()(layer3)
layer5 = layers.Dense(512, activation="relu")(layer4)
action = layers.Dense(num_actions, activation="linear")(layer5)
return keras.Model(inputs=inputs, outputs=action)
Note the aggressive downsampling in the first conv layer: a stride of 4 and a kernel size of 8. Note also the lack of max pooling.
Note layer 4 flattens the final convolution filters into a flat vector to feed into the dense layers.
Note the final layer has a linear activation, so not outputting a probability (as he mistakenly says in the video) - that would need a softmax activation.
14.107 DQN Loss function
Reviews the loss function equation from 12.110 above.
Then walks through the training step in the implementation.
First we get a random selection from the replay buffer:
indices = np.random.choice(range(len(done_history)),
size=batch_size)
# Using list comprehension to sample from replay buffer
state_sample = np.array([state_history[i] for i in indices])
state_next_sample = np.array([state_next_history[i] for i in indices])
rewards_sample = [rewards_history[i] for i in indices]
action_sample = [action_history[i] for i in indices]
done_sample = tf.convert_to_tensor(
[float(done_history[i]) for i in indices]
)
Then we have to generate the updated Q values:
# Build the updated Q-values for the sampled future states
# Use the target model for stability
future_rewards = model_target.predict(state_next_sample)
# Q value = reward + discount factor * expected future reward
updated_q_values = rewards_sample + gamma * tf.reduce_max(
future_rewards, axis=1
)
# If final frame set the last value to -1
updated_q_values = updated_q_values * (1 - done_sample) - done_sample
MYK fluffs the explanation of the masks a bit. The idea here is that we only calculate the loss on the actions taken, we don’t bother with the values for the actions that were not taken.
We do this by creating a set of one-hot vectors which will have 1 in the location of the action taken, and 0 for all other actions. This one-hot vector is then multiplied with the Q value vector. So all the Q values for actions not taken will be zeroed out and ignored.
That’s this bit of the code:
# Create a mask so we only calculate loss on the updated Q-values
masks = tf.one_hot(action_sample, num_actions)
with tf.GradientTape() as tape:
# Train the model on the states and updated Q-values
q_values = model(state_sample)
# Apply the masks to the Q-values to get the Q-value for action taken
q_action = tf.reduce_sum(tf.multiply(q_values, masks), axis=1)
# Calculate loss between new Q-value and old Q-value
loss = loss_function(updated_q_values, q_action)
The loss function they use is: loss_function = keras.losses.Huber()
Finally we do backpropagation:
# Backpropagation
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
14.109 DQN Code Review
Reviews the end to end process of training and running the agent.
The one issue MYK found in training was the size of the replay buffer. In the Nature paper, the buffer was a million units large. That takes a lot of RAM… On the Keras script it was 100,000.
This didn’t work on a 16GB RAM machine. It did work on Google Colab and a 24GB machine.
Shows the training results, it managed to do well on Breakout. But on Breakwall it struggled.
Walks through the script to load the pretrained model and use it to play the game.
Week Five: State of the Art
15.102: State of the Art Players
Reviews progress in game playing after DQN.
Invites you to apply what we learned from the DQN agent to assess the developments in the papers published since then. How did they advance the network architectures? How do they compute the ground truth? What does the runtime look like?
Introduces the papers mentioned in the reading list here: cm3020 Topic 03: Reinforcement Learning (Game Playing)
Suggests Agent57 in Badia et al: Agent57: Outperforming the Atari Human Benchmark ends the Atari work as it plays games better than humans.
Turns to Starcraft in Arulkumaran: AlphaStar: An Evolutionary Computation Perspective, notes that it draws on evolutionary computation as well as deep learning/RL etc.
OpenAI have been focusing on DOTA instead. Discusses the Togelius: The Mario AI Championship paper and how the community evolved to look at wider range of games.
15.104: Ethics of Game Playing AI
Looks at the criticism of AI vs human competitions in Canaan: Leveling the Playing Field: Fairness in AI versus Human Benchmarks
Is competition only fair if the artificial agent has the same constraints as a human?
The paper proposes six dimensions of fairness:
Perceptual: Do the two competitors use the same input space?
Motoric: Do the two competitors use the same output space?
Historic: Did the two systems spend the same amount of time on training?
Knowledge: Do the two systems have the same access to declarative knowledge about the game?
Compute: Do the two systems have the same computational power?
Common-sense: Do the agents have the same knowledge about other things?
Suggests a more moderate view is Justesen et al: When are we done with games?
Turns to the impact of superhuman players on game players. The Go player retired after losing to AlphaGo.