Jurafsky Martin Chapter 14: Dependency Parsing
Metadata
Title: Dependency Parsing
Number: 14
Related Lectures
Manning 15.1: Dependency Parsing Introduction
Manning 15.2: Greedy Transition Based Parsing
Manning 15.3: Dependencies Encode Relational Structure
Terminology and Example
In dependency grammars phrasal constituents and phrase structure rules do not play a direct role. Instead the syntactic structure of a sentence is described solely in terms of directed binary grammatical relations between the words.
Relations among the words are captured in binary asymmetric relations (Arrows, arcs, dependencies). The arcs go from a head (governer, superior, regent) to a dependent (modifier, inferior, subordinate).
Typically dependencies form a tree (connected, acyclic, single head), with a root node marking the head of the whole sentence. The lecture mentions that it’s common to add a pseudo root node as a parent of the sentence head. This makes it cleaner, since every word in the sentence has a single parent (including the head), so you can model parsing and evaluating parsers as finding the correct parent for every word in the sentence.
The arcs are typically labelled with the name of grammatical relations (eg subject, prepositional object, apposition etc.). So we call this a typed dependency structure.
Here is an example:
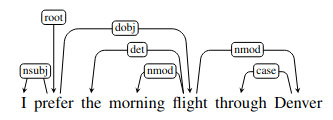
And a side by side with the phrase structure representation:
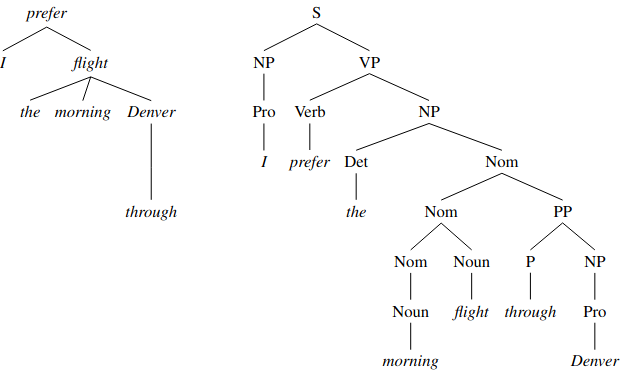
Note that there are no nodes in the dependency tree that represent constituents or categories, its internal structure consists solely of directed relations between lexical items in the sentence.
These relations directly encode information that can be buried in complex phrase-structure grammars. For example in the example - look at the arguments to the verb “prefer”. The dependency parse makes them very clear, while the phrase structure parse keeps them very distant.
Likewise the modifiers of “flight”, are linked directly in the dependency structure.
Original CFGs had no formal notion of ‘heads’ of sentences, but work there has evolved and modern linguistic theory and statistical parsers do use the notion of ‘head’ extensively and apply head finding rules. So you can extract dependencies from the phrase structures. But if you try to go the other way you’ll often find different representations of phrase structure result (see lecture 1).
Dependency grammars are also great at dealing with free word order. In many languages words can float freely, and in a phrase structure grammar you would need separate rules for every location. But in a dependency grammar abstracts from that.
The other great motivation of dependency grammars is that the head-dependent relations approximate the semantics of predicates and their arguments. This makes dependency parses useful for many applications like QA, information extraction, and coreference resolution.
Dependency Relations
The basis for dependency structures is the traditional linguistic notion of grammatical relation. The arguments to these relations consist of a head and a dependent. These are already used in extended CFGs to denote eg the central noun in a noun phrase (with the other words in the phrase dependent on that head), but the relations are explicit in dependency grammars.
Dependency grammars allow us to classify grammatical functions or relations that the dependent plays in respect to its head. These include subject, direct object, indirect object.
Among the taxonomies of such relations, the Universal Dependencies project aimed to provide cross-linguistic standards that are computationally useful.
The core set can be divided into two categories:
clausal relations, describing syntactic roles with respect to a predicate (often a verb).
modifier relations, categorizing ways that words can modify their heads.
| Clausal Argument Relations | Description |
|---|---|
| NSUBJ | Nominal subject |
| DOBJ | Direct object |
| IOBJ | Indirect object |
| CCOMP | Clausal complement |
| XCOMP | Open clausal complement |
| Nominal Modifier Relations | Description |
|---|---|
| NMOD | Nominal modifier |
| AMOD | Adjectival modifier |
| NUMMOD | Numeric modifier |
| APPOS | Appositional modifier |
| DET | Determiner |
| CASE | Prepositions, postpositions and other case markers |
| Other Notable Relations | Description |
|---|---|
| CONJ | Conjunct |
| CC | Coordinating conjunction |
And some examples:

Dependency Formalisms
A dependency structure can be represented as a directed graph \(G = (V,A)\), with a set of vertices \(V\), and a set of ordered pairs of vertices \(A\). In English \(V\) will usually be words, maybe punctuation too. In other languages you might need to break down the morphology.
Constraints on the graph structure come from different grammatical formalisms. EG they may require the graph to be connected, have a designated root, acyclic or planar etc. Typically we restrict to rooted trees ie:
There is a single designated root node that has no incoming arcs.
With the exception of the root node, each vertex has exactly one incoming arc.
There is a unique path from the root node to each vertex in \(V\).
So each word has a single head, the structure is connected, and there is a single root from which you can follow a unique directed path to each word in the sentence.
Projectivity
An important issue to understand in looking at dependency grammars and parsing is projectivity. An arc from a head to a dependent is projective if there is also a path from the head to every word that lies between the head and the dependent in the sentence. A tree is projective if all its arcs are projective.
There are many valid constructions which don’t have this property, for example:
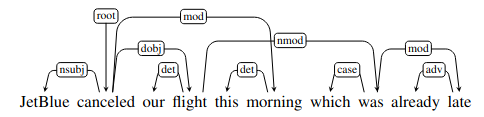
The arc from flight to was is non-projective. You can see that a dependency tree is projective if it can be drawn with no crossing edges, while here thre are crossing edges.
The problem is that many dependency treebanks were generated from phrase structure treebanks. These are always projective, and so incorrect in cases of non-projective dependencies.
Similarly, many families of parsing algorithms are incapable of generating non-projective parse trees. Again this means their output will be incorrect in non-projective sentences like the example.
There are graph-based parsing approaches that try to overcome this.
Dependency Parsing
The chapter walks through two main approaches to dependency parsing.
Transition-Based Dependency Parsing
This is an approach that descends from work in parsing programming languages (shift-reduce parsing).
You maintain a stack on which you build the parse, a buffer of tokens to be parsed, and a parser that takes actions on the parse based on predictions from an oracle.
The parser walks through the sentence left to right, successively shifting items from the buffer to the stack. At each step, you examine the top two items on the stack, and the oracle makes the decision about what transition to apply.
Those transitions include intuitive options like:
Assign the current word as the head of a previously seen word (assert a
LeftArcand pop the second word from the stack)Assign some previously seen word as the head of the current word (assert a
RightArcand pop the top word from the stack)Postpone a decision and store the current word to deal with it later (remove it from the buffer and push it on the stack)
You can see a visual representation of the parser in the book:
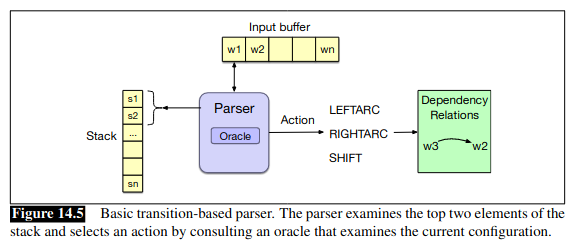
The chapter walks through an example in some detail.
The big question then is how do you get an oracle capable of making the right decision? The chapter walks through ML based approaches. First a classical feature-based approach where we develop features like POS, word, location.
Manning’s lecture (1) introduces other relevant features, bilexical affinity (but issues with sparse data), dependency distance, intervening material (dependencies rarely span intervening verbs and punctuation other than commas), valency of heads (how many dependents on which side are usual for a head). His second lecture walks through
MaltParserin a lot of detail.The chapter also shows that it’s relatively simple to train a neural classifier to act as an Oracle. You encode the sentence, then take the representations of the first two stack items and the next buffer token and pass them through a feedforward network with a softmax output over the possible actions.
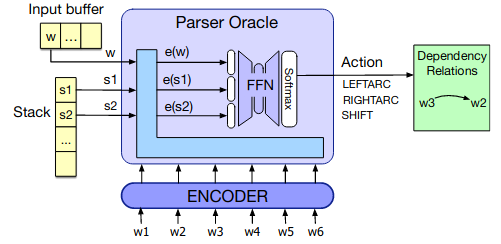
The chapter walks through some more advanced techniques like arc eager parsing and using beam search.
Graph-Based Dependency Parsing
The other important family are graph-based methods. These are more accurate than transition-based parsers, especially on long sentences. They don’t make greedy local decisions, so deal better with long-range dependencies.
They can also produce non-projective trees.
Essentially, graph-based dependency parsers search through the space of possible trees for a given sentence for a tree (or set of trees) that maximize some scoring function.
They encode the search space as directed graphs and then use methods drawn from graph theory to search the space for possible solutions.
So given an input sentence \(S\) we’re looking for the best dependency tree in \(\mathcal{G}_S\), the space of all possible trees for that sentence, that maximizes some score:
\[\hat{T}(S) = \underset{t \in \mathcal{G}_S}{\mathrm{argmax}} \; \mathrm{Score}(t,S)\]
We tend to simplify by saying that we’ll treat the score of a graph as the sum of scores of its edges. So the algorithm has to find a way of scoring an edge, and then finding the best tree given the all the edge scores.
The second step is equivalent to finding a Maximum Spanning Tree of a densely connected graph, where all edges are scored. So we first calculate all the edge scores of a densely connected graph represnting all possible edges. Then we find a maximum spanning tree.
The chapter walks through the process in detail, and shows feature-based and neural approaches for assigning scores to edges.
Evaluation
Finally the chapter presentes evaluation. The metrics typically used are Labeled Attachment Score (LAS) and Unlabeled Attachment Score (UAS).
LAS refers to the proper assignemnt of a word to its head along with the correct dependency relation.
UAS simply looks at the correctness of the assigned head, ignoring the relation.
Label accuracy score (LS) is the percentage of tokens with correct labels, ignoring where the relations come from.
Beyond this we might look at precision/recall for particular labels, and use confusion matrices to see where we’re going wrong.
Dependency Relations and Information Extraction
Not in this chapter of the book, but Manning’s lecture 3 shows how dependency trees can be adapted to more directly capture relations that we like to extract in information extraction applications. He also shows why we look at syntax at all in relation extraction tasks - it makes it much easier as relations are often captured in one or two steps of a dependency tree, while linear distance in the sentence might be much longer.