Combinatory Categorical Grammar
As presented in Jurafsky Martin Chapter 12: Constituency Grammars
Categorical Grammar was an early lexicalized approach to grammar modelling. An important modern extension is combinatory categorical grammar. The chapter reviews both.
Categorical Grammar
The categorical approach consists of three main elements: A set of categories, a lexicon that associates words with categories, and a set of combination rules that govern how categories combine in context.
Categories
The elements of the set \(\mathcal{C}\), Categories, are either atomic elements, or functions that take a single argument and yield a desired category.
The first case is simple, \(\mathcal{A} \subseteq \mathcal{C}\), where \(\mathcal{A}\) is a given set of atomic elements.
For the second we need to understand the slash notation in this context. (X/Y) is a function that seeks a constituent of type Y to its right and returns a value of X. (X\Y) is the same except it seeks the constiuent to its left.
So we add to our set of categories (X/Y), (X\Y) \(\in \mathcal{C}\) where X,Y \(\in \mathcal{C}\).
The set of atomic categories is small, it includes sentences, noun phrases. Functional categories include verb phrases and complex noun phrases.
Lexicon
The lexicon consists of assignments of categories to words. Words can be assigned to multiple categories. Categories may be atomic or functional. For example flight: N; Miami: NP; cancel: (S\NP) / NP.
Nouns are assigned to atomic categories, reflecting their role as arguments to functions.
Take the complex example of cancel though, a transitive verb. This is assigned to a function category. The function seeks a NP on its right and returns a function with the type (S\NP). That function can, in turn, combine with a NP on its left, to yield a S.
This is a solution to the subcategorization problem discussed in English Grammar Rules (Jurafsky Martin), but the information here is rich, computationally useful, rather than a lot of flat rules.
The functions can get more complex, for example a ditransitive verbs like give expect two arguments after the verb. We can express this with the category: ((S\NP)/NP)/NP.
Rules
Rules specify how functions and their arguments combine. There are two rule templates that form the basis for all categorical grammars:
Forward function application:
\[X/Y \; Y \Rightarrow \; X\]
Backward function application:
\[Y \; X \backslash Y \Rightarrow \; X\]
We can illustrate function applications growing down from the intial words like this:
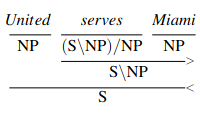
We can add the conjunction metarule:
\[X \; CONJ \; X \Rightarrow \; X\]
Now let’s derive a more complex example:
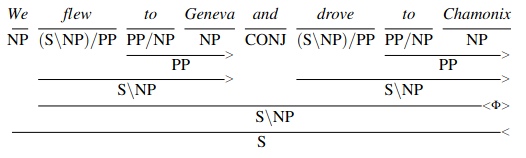
Note the fundamental lexical approach here, the grammatical facts are largely encoded in the lexicon. We are moving information essentially from the grammar rules to the lexicon.
But the expressive power so far is the same. To get more we need to be able to include operations that operate over functions. This gets us to a CCG.
Combinatory Categorical Grammar
CCGs include operations over functions that we need to get more expressive power.
The first pair allow us to compose adjacent functions:
Forward composition:
\[X/Y \; Y/Z \Rightarrow \; X/Z\]
Backward composition:
\[ Y \backslash Z \; X \backslash Y \Rightarrow \; X \backslash Z\]
The next operation is called type raising, which takes a category and converts it to a function that seeks as an argument a function that takes the original category as its argument.
\[ X \Rightarrow \; T/(T\backslash X)\]
\[ X \Rightarrow \; T\backslash(T/X)\]
What does this get us?
First, it starts to produce a left-to-right, word-by-word derivation that more closely mirrors human processing of English.
Second, it enables derivations like the following, which make use of non-constituent elements like ‘United serves’. This ability provides CCG with the ability to co-ordinate phrases that aren’t constituents.

Finally it can handle long distance dependencies, like this:

See the book for a full explanation.
CCGbank is a mapping of the Penn Treebank to CCG form. It can be used to train parsers.