Jurafsky Manning Lecture Summaries: Topic 17: Information Retrieval
Relating to cm3060 Topic 08: Information Retrieval
17.1: Introduction to IR
Information Retrieval (IR) is finding material (usually documents) of an unstructured nature (usually text) that satisfies an information need from within large collections (usually stored on computers).
There are many scenarios, web search, e-mail search, searching your laptop, legal IR, corporate knowledge bases.
The basic assumptions of IR are as follows:
We have a collection, a set of documents over which we are going to do retrieval. We can assume they are static for now.
Our goal is to retrieve documents with information that is relevant to the user’s information need and helps the user complete a task.
We can illustrate it with this diagram:
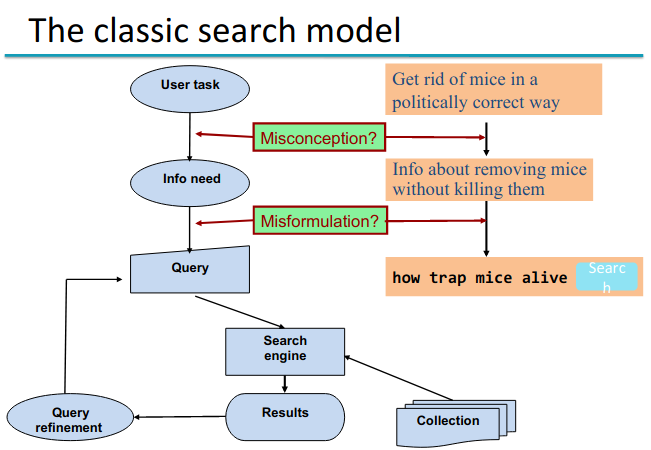
At the start we have some task that the user wants to perform. To achieve the task I feel I need some more information. This is my information need, and how we assess information retrieval systems.
We need to translate the information need into something that the computer can operate on.
What can go wrong in the process? I might have a misconception that interferes with the identification of the information need - I might not understand the information need I actually have to complete my task. Or I might have a misformulation I might poorly translate my information need into a query.
We’ll talk more about evaluation later, but need a rough sense to understand the whole process. We can broadly evaluate through precision and recall. Precision in this context is the fraction of the retrieved docs that are relevant to the user’s information need. Recall is the fraction of relevant docs in the collection that are retrieved.
For these measures to make sense they have to be evaluated against the information need. We don’t evaluate against the query, since the systems might be deterministic and hence precision would be 100% against the query itself. This means that if the user formulates a bad query, this will lower the precision in the evaluation. More details later…
17.2: Term-Document Incidence Matrices
Let’s start with a concrete example. We want to know which of Shakespeare’s plays contain the words Brutus, and Caesar, but not Calpurnia.
One approach would be go grep, searching through the text exhaustively. So we could grep the plays for Brutus and Caesar and then strip the lines containing Calpurnia.
Now our computers are fast enough that you could actually do this and it would be fast. But as a general solution it falls flat.
Once the corpus gets large we can’t do a linear scan. It also falls down with more complex operations like finding words near each other.
Finally we just can’t do ranked retrieval with linear scan methods.
We’ll start improving the grep approach with a term-document matrix. Here the rows are words, or terms, and the columns are documents.
An incidence matrix is a term-document matrix with boolean values where 1 indicates the presence of the term in the document.
So concretely we could take the row representing Brutus (say 110100), the row for Caesar (say 110111), and the complement for Calpurnia (say 101111), then we could perform a logical AND on the vectors.
But this doesn’t work when we get to a bigger collection. Let’s say we have a million docs (N) with a mean of 1000 words per doc.
Let’s assume an average of 6 bytes per word including spaces/punctuation, that’s 6GB of data in the docs.
Let’s say there are M = 500k distinct terms among these docs.
Already we cannot build this matrix. We have 500k terms x 1M docs, that’s half-a-trillion booleans, but no more than 1 billion 1s. The matrix is extremely sparse.
so what’s a better representation? We only record the 1s. So the Term-doc matrix is an important conceptual data structure that we will use throughout as a reference in IR, but physically we don’t actually use it to store data.
17.3: The Inverted Index
This is the key data structure that underlies all modern IR systems. It exploits the sparsity of the term-document matrix, and allows for very efficient retrieval.
It’s structured like this:
- For each term t, we must store a list of all documents that contain t.
- Each document can be identified with a docID, which is just a serial number.
Can we use fixed-size arrays for this? Not really, it would be inefficient and hard to make dynamic.
So we use variable length arrays, which we call postings lists. On disk these should be continuous, in memory they could be linked lists or variable sized arrays with the usual trade-offs.
The dictionary is the set of terms which would have as a key the term, and their value would be the posting list for that term.
One occurence of a document-term occurence is called a posting, and the sum of all the postings lists are the postings.
The postings lists are sorted by docID.
Globally, the dictionary size is relatively small, but must be in memory. The postings are large, but for a small-scale enterprise search engine can be stored on disk.
The construction process is as follows:
We start with a collection of documents to be indexed. We assume these have been converted from their source type (Word, pdf etc) to text strings.
First we need to tokenize, convert the docs to lists of tokens. Often these won’t be the exact words that occur in the doc. There might be linguistic models that we would use to normalize the tokens.
These modified tokens will be fed into an indexer to construct the index.
The text processing step involves decisions on how to deal with apostrophes, hyphens etc. Normalization, stemming etc from cm3060 Topic 02: Basic Processing, stop words etc. Modern indexes are efficient enough that we don’t typically use stop words any more in IR.
For the indexing process, our input is a list of normalized terms in the order they occur in each document, along with their docID.
First we sort as primary key by the terms, putting them in alphabetical order. Then we sort using docID as a secondary key, where we have the same term appearing in multiple docs. This is an expensive step.
Now we do a consolidation of the result. Multiple occurences of a term in a doc are merged, then we split into a dictionary and postings, while recording the document frequency for later use. We end up with this:
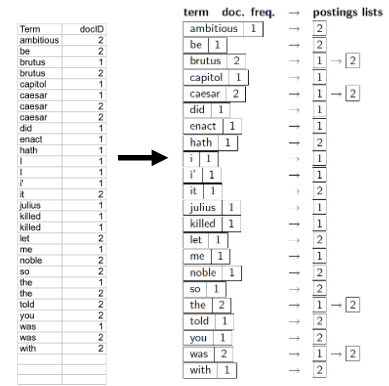
Since we’ve sorted already we can build the postings list in order easily now.
Where do we pay in storage? The dictionary is in the order of the number of unique terms, the postings are bounded by the number of words in the collection.
17.3: Query Processing with an Inverted Index
First we’ll look at the details of a sample query, then at the kinds of queries we can process.
For a single word query the process is straightforward, we just retrieve its postings list.
What about a boolean and query. We locate both words in the dictionary, get their postings lists, and then merge the two lists. But this is a bit misleading in the case of AND, we’re doing intersection not union.
The merge algorithm family refers to the operations you can perform on sorted lists, so it’s applied even if we’re doing intersection.
The merge operation is as follows:
Walk through the two postings simultaneously, in time linear to the total number of posting entries.
We have two pointers, one for each list. We ask if they are pointing at the same docID. If not we advance the one with the smaller docID. If yes, we put the docID in a result list and advance both.
We stop when one of the lists is exhausted and return the results list.

17.4: Phrase Queries and Positional Indexes
Phrase queries have, in practice, been the most important kind of extended Boolean query. They require some extension of the inverted index approach we’ve followed so far.
Often we don’t want to query for single word units, we want multi-word units, like “Information Retrieval”, “Stanford University”. The standard syntax for this is inverted quotes around the phrase.
This syntax has proven to be easily understood by users, one of the few ‘advanced search’ ideas that works in practice.
In addition to explicit phrase queries, there are many implicit phrase queries, where users will search for San Francisco where what they mean is "San Francisco". In modern search engines identification of implicit phrases is a key area of work.
It no longer suffices to just store the term: docs posting lists. How do we do it?
Biword Index
A first approach would be a biword index. So we could index every consecutive pair of terms in the text as a phrase. So for example with the text “Friends, Romans, Countrymen” we could index “friends romans” and “romans countrymen”. Then each byword becomes a dictionary term.
Now two word phrase querying is immediate. We can kind of handle longer phrases too, we could treat “Stanford University Palo alto” as being "stanford university" AND "university palo" AND "palo alto". But without the docs we can’t verify that the boolean query match does represent the actual phrase. So we could get false positives.
The other issue is index blowup due to the bigger dictionary. It’s big even for biwords, and not practical beyond that. So this is not the standard solution, but can be a component of a solution.
Positional Index
The standard solution instead is to move to a positional index. Here we store in the postings, for each term, the position(s) in which tokens of it appear.
So now our data structure looks like this:

Each doc is now a list itself, containing positions in the doc in which it occurs.
We can still use a merge algorithm for phrase queries, but now we have to do it recursively, where we both intersect the document ids, and then also check that there are compatible positions for the words occuring in the phrase.
So we need to deal with more than just equality, we have to check that the terms are sequenced correctly.
First we extract inverted index entries for each distinct term in the phrase.
Then we merge their doc:position lists to enumerate all positions with the phrase we’re after (eg “to be or not to be”)
We do it by progressively working along the phrase query, first checking for candidate matches for the first two terms, then filtering those candidates on the next two and so on
For each pair of terms, First we can eliminate documents that don’t appear in all the postings lists, by advancing pointers until we have a match at the docID level.
When we get to a match at the docID level, we have to recurse, and do another merge algorithm for the positions within the postings list. Where we find a candidate match (the tokens in the right sequence) we add them to a list of candidate matches. We go back up to the doc level when we’ve exhausted the positions.
This works even when the words are not offset by one, you can do it with proximity searches too.
The cost of positional indexing is that our postings list gets a lot larger, now we store offsets of tokens within docs. But it’s now completely standard to use them, because they are so powerful.
The size of the index now depends on the average size of the documents. It remains smaller than, but approaching 35-50% the size of the original text.
Combining the Two
You can profitably combine positional indices and biword indices. If you look at the query stream from your search engine you see some popular searches occur over and over again (eg people’s names). Especially bad when you are searching for something like “The Who”, where the postings lists are really large.
So you can mix and match, you can create biword indices of common biword searches. You can do it dynamically, keeping a cache of common queries.