CS253 Lecture Summaries: Part XI Transport Layer Security
The core problem: HTTP is not “secure”. Why?
At its heart, HTTP sends plain text over the networks, so anyone on the network can see the message.
Let’s say a passive attacker on the network wants to see the message. They just look at the message and send it on. They see the response, including cookies, and send that on too.
An active attacker may modify the request or response as they go by. Let’s say they add some Javascript to the response before sending it on to the client.
What is the threat model? Network attackers control network infrastructure like routers or DNS servers.
Network attackers may eavesdrop, inject, block, or modify packets.
Potential network attackerrs occur anywhere there is an untrusted router or ISP:
wireless networks at cafes or hotels
border gateways between countries
Our goal: to secure communication against these attackers. We want:
privacy - no eavesdropping
integrity - no tampering
authentication - no impersonation
Our approach is Transport Layer Security and when this is used with HTTP we have HTTPS or Hyptertext Transfer Protocol Secure.
HTTPS keeps browsing safe by securely connecting the browser with the website server.
HTTPS relies on TLS encryption to secure connections.
TLS is used with web traffic, email, instant messaging, voice over IP, and many other protocols, not just HTTPS.
We need a set of primitives to communicate securely with a server.
Anonymous Diffie-Hellman key exchange
This is anonymous because we don’t do any authentication of the server we’re talking to. This will not protect us from an active attacker who’s going to modify packets - it just protects us from passive attackers.
We have a cyclic group \(G = \{ 1, g, g^2, g^3, \dots, g^{q-1} \}\) G is a number that is publicly known, defined by a standard. There are q members of the group.
We can do group operations on this group, which means we can do exponentiation. The cyclic group is defined such that doing the log of an element is computationally infeasible.
The client and the server will pick a group element randomly, identified by the range \(\[1,q\]\). Let’s call the client’s a and the server’s b.
The client will send \(A = g^a \in G\) to the server, and the server will send \(B = g^b \in G\) to the client.
In the end we’ll end up with \(DHKey = g^{ab}\) which is a shared key known to the client and the server, but which any passive attacker can’t find out.
How do they get it? Well the client does \(B^a\), ie \(\(g^b\)^a\) and the server does \(A^b\), ie \(\(g^a\)^b\).
This is called anonymous key exchange. But there’s still a problem. The client doesn’t know with which server it performed key exchange. It’s possible that the client securely derived a key with the network attacker rather than the server.
The communication is technically private (secure against eavesdropping) but it lacks authentication.
Key idea: without authentication you can’t actually have privacy.
Authentication
Goal: If the client could authenticate the server it is performing key exchange with, then it could securely derive a shared key with that, and only that server.
Solution: use public-key cryptography for authentication.
Recap: we have a triple of algorithms: \(\(G, S, V\)\)
G - the generator, which gives us a public key and secret key.
S - the signing algorithm, which takes the secret key and a message and returns a public tag for the message.
V - the verifier, which takes a public key, a message, and a tag and checks the validity of the tag for the given message.
Algorithm properties:
Correctness \(V\(pk, x, S\(sk, x\)\)=accept\) should always be true.
Security: \(V\(pk, x, t\) = accept\) should almost never be true when x and t are chosen by the attacker.
Now we can adapt Diffie-Hellman to become an authenticated DH key exchange as follows:
The server generates a public key and secret key, broadcasting its public key to the client.
We do the same as before, client generates a and sends \(g^a\) and server decides b.
Now the server takes a transcript of the exchange so far - (ie that the client has sent \(g^a\) and \(g^b\)) - and signs it with it’s secret key, producing a tag.
Now the server sends back \(g^b\) along with the tag. The client first verifies the tag, was that correct? If so it will derive the shared key.
Note that this is not a 2-way authentication, the server doesn’t authenticate the identity of the client. This latter auth happens at the web application layer since the user can now safely log in.
How does the client get the server’s public key?
We can’t include all public keys in the browser - too large and changing a list.
We can’t send the public key to the client during the key exchange - as now we’re back to the same problem as anonymous key exchange. The attacker could send a bogus public key.
The solution: certificate authorities - an entity that issues digital certificates.
A certificate certifies that a named subject is the owner of a specific public key:
“I certificate authority, certify that subject is the owner of the public key key”.
If we trust a few CAs, and they verify the server, we can trust the server’s key.
Certificates
You can look at a certificate by clicking the lock in the browser and navigating through to the certificate.
Some points of interest: The Common Name is what the browser will check.
It is usually an explicit name but can be a wildcard, eg *.google.com. The * does not match the . character, and must occur in the leftmost subdomain component.
Alternate subject name can include other domains in the one certificate.
Who does your browser trust? You can look it up. In Firefox it’s in the browser itself, you can see it in the settings.
For others, like chrome, they will look at a store in the operating system. Employers can add their own CA to this store so they can inspect all the traffic.
Here’s an illustration of how the certificate exchange works:
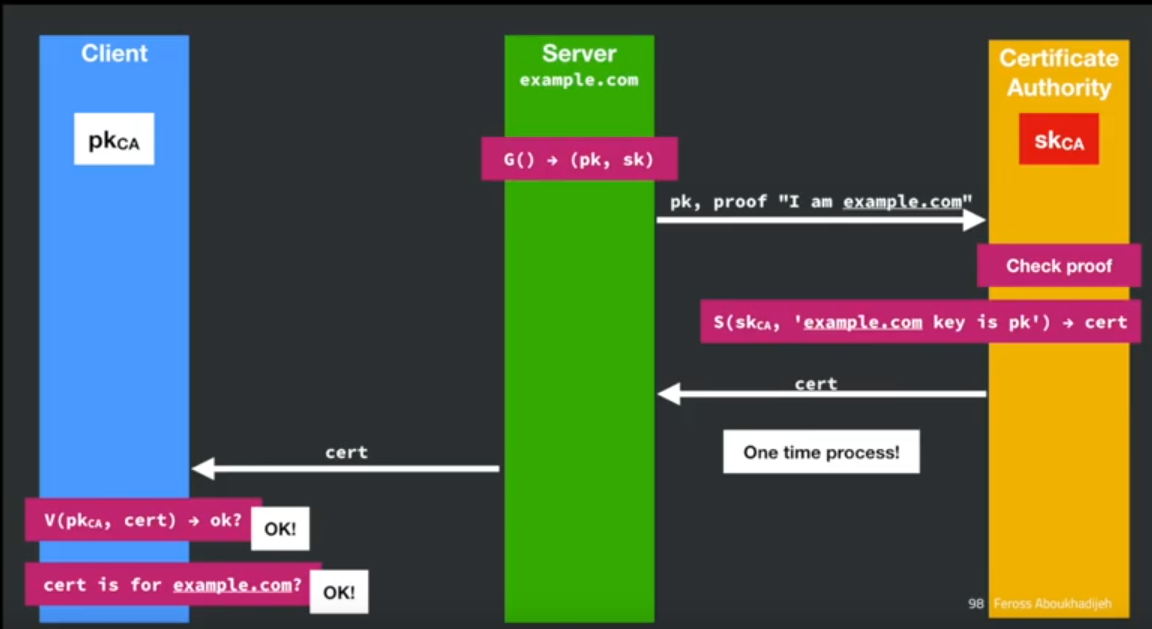
Let’s encrypt is the fastest growing CA, because it’s free. Funded by Mozilla and others. They provide a command line tool that you can use to talk to the Let’s Encrypt and get you your certificate.
TLS 1.3
TLS 1.3 is the latest version of TLS which replaces TLS 1.2. 1.2 replaced TLS 1.1, 1.0, and SSL 3.0, 2.0, 1.0 (SSL is often used interchangeably with TLS, and predated it).
Now browsers will only talk to servers speaking 1.3 essentially. Previous versions had serious flaws and no longer function.
Goal: provide privacy and reliabilty between two communicating applications.
Two phase protocol:
Handshake protocol - Establish a shared secret key using public key cryptography.
Record protocol - Transmit data using the negotiated key.
TLS 1.3 properties:
Nonces prevent replay of an old session.
Forward secrecy server compromise does not expose old sessions.
identity protection - certificates are sent encrypted. But this is incomplete - you can still tell that you send the data to a particular IP address.
one-sided authentication - client authenticates the server using the server’s certificate
TLS has support for mutual authentication “client certificates” but it is rarely used.
Lock icon
Only show the lock if every element on the page is fetched with HTTPS.
For all elements:
HTTPS certificate must be issued by a CA trusted by browser
HTTPS certificate must not be expired
HTTPS certificate CommonName or SubjectAlternativeName must match the URL.
Certificate Chains
How many CAs are there?
Top-level CAs, around 60
Intermediate CAs, around 1200
If any single CA is compromised, security of all websites on the internet could be compromised, oh no!
HTTPS Attack: TLS Strip
Commonly known as ‘ssl strip’ - the earlier name of TLS.
Most servers which support HTTPS implement an HTTP to HTTPS redirect.
When user omits protocol, browser assumes http.
What if the attacker intercepts the first unencrypted request? They can man-in-the-middle all the traffic to rewrite the html to keep the user on the http version.

How do we prevent this?
The solution is HTTP strict transport security (HSTS).
To defend against the TLS strip attack, the server tells the browser “no matter what protocol the user specifies, always use HTTPS”.
Strict-Transport-Security: max-age=31536000
Use HTTP header to force browser to use HTTPS for one year!
Downside - trust on first use model means that first visit to the site is still not secure against man-in-the-middle.
Should clearing history clear the HSTS list? Privacy vs security.
One solution to the trust on first use problem is to use an HSTS preload list, browsers offer to hardcode sites that always want to be https only, so we send the header like this:
Strict-Transport-Security: max-age=63072000; includeSubDomains; preload
Must include both subdomain and preload options. Then browser hardcodes our security policy. But it’s difficult/impossible to remove a domain after that has happened.
Certain TLDs added the whole TLD to the preload list (eg .dev).
You should do this for all your sites though. Check and register here