Stream Ciphers Part Two (Boneh)
Real-world Stream Ciphers
Old example: RC4 (1987)
Variable sized seed (eg 128 bits) - expands to eg 2048 bits - used as the internal state of the generator.
Runs a loop where every iteration produces 1 byte of output.
Used in HTTPS and WEP. Some weaknesses though (don’t use in new projects):
Bias in initial output - probability that early byte is 0 is 2/256. Recommended to ignore first 256 bytes of the output.
Probability of (0,0) is also biased. It should be 1/256 squared, but it’s 1/256 squared + 1/256 cubed. This starts after several gigabytes of data.
Related key attacks (eg the WEP attacks).
Old example (hardware): Content Scrambling System - CSS (badly broken)
Used to encrypt DVD movies on disk for example. Also bluetooth.
Based on a mechanism called Linear feedback shift register (LFSR).
Here you have a register with a set of cells containing a bit. There are a set of taps into the register (a few target cells) that feed into an XOR.
Every clock cycled the bits in the register shift right, the final bit drops off, and the result of the XOR is added as the first bit in the register.
The seed is the initial state of the LFSR.
In CSS the seed is 5 bytes (40 bits)
There are two LFSRs, one 17 bit, the other 25 bit.
The key is generated by starting with 1 and concatenating the first two bytes of the 17 bit LFSR.
Similar with the second, start with a 1 and concatenate the last three bytes of the 25 bit LFSR.
The LFSRs are run for 8 cycles (produce 8 bits of output), which is then fed into an adder which does addition mod 256.
That outputs one byte per round, which is used to XOR the the corresponding byte of the DVD file to decrypt it.
This will run very fast. But it’s easy to break in \(2^{17}\) time.
We know the start of the plain text file (the header), say 20 bytes. If we XOR that with the first 20 bytes of the encrypted data we get the first bytes of the cipher output.
Now we try all \(2^{17}\) possibilities of the first 17 bit LFSR. For each value we run the LFSR for 20 bytes.
We subtract each of these from the known output of the LFSR that we got earlier. If we’re correct we’ll have the first 20 byte output of the second LFSR.
It turns out it’s easy to tell whether a 20 byte sequence was generated by an LFSR. If it’s not, then we know our guess is wrong and we move on.
Once we get the right sequence, we know both, and can decrypt the rest of the stream.
More modern examples of stream ciphers
eStream Project: Salsa20
Concluded in 2008, produced 5 different stream ciphers.
In these ciphers we have a seed, and also a nonce, a non-repeating value for a given key. This gives us:
\(PRG: \{0,1\}^s \times R \rightarrow \{0,1\}^n\)
The PRG takes a seed and a nonce and produces an ouptut that’s much bigger than the seed.
The nonce will never repeat so long as the key is fixed. IE the property is that the pair \((k,r)\) is never used more than once. Then the encryption algorithm is:
\[E(k,m;r) = m \oplus PRG(k;r)\]
We can re-use the key, because the nonce makes the pair unique.
Some ciphers are designed for software (they are intended to be fast in software), others like CSS are designed for hardware, to make hardware implementation cheap and fast.
One eStream cipher: Salsa 20 is designed for both. How does it work?
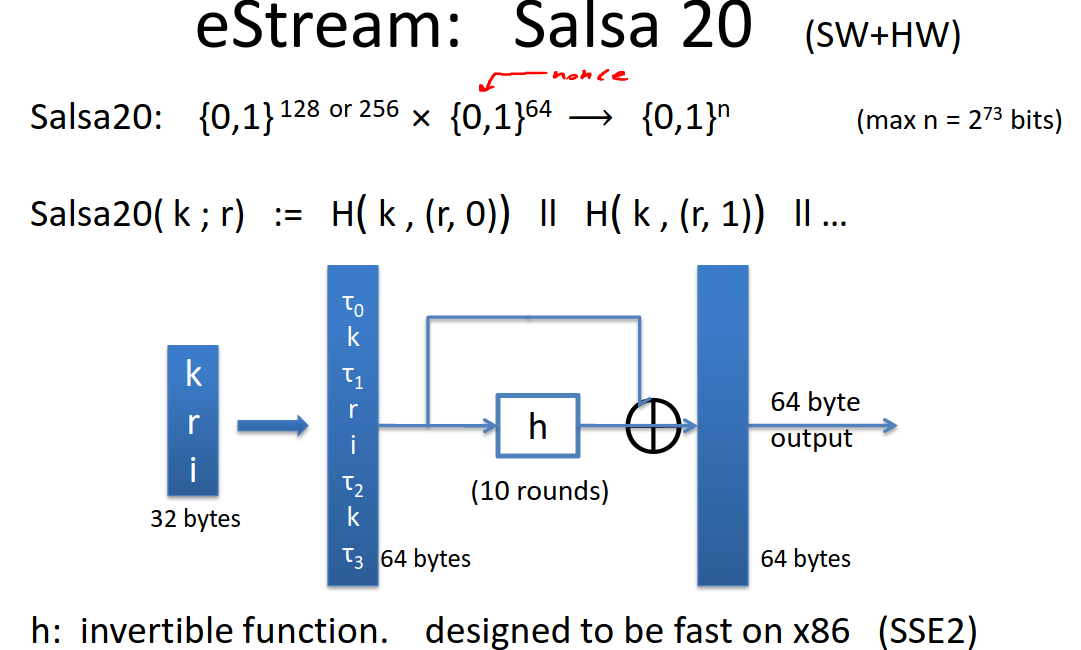
It takes 128 or 256 bit seeds (ie \(\{0,1\}^{128}\) or \(\{0,1\}^{256}\)), and a 64 bit nonce ( \(\{0,1\}^{64}\)) and produces an output that is max \(2^{73}\) bits long:
\[Salsa20: $\{0,1\}^{128} \times $\{0,1\}^{64} \rightarrow $\{0,1\}^{n}\]
The function itself is defined as follows:
\[Salsa20(k;r) := H\left( k,(r,0) \right) || H \left( k,(r,1) \right) || \dots\]
The function \(H\) takes three inputs, the seed \(k\), the nonce \(r\), and a counter that increments from step to step. It produces a step in the output sequence that is then concatenated together for an output as long as we want.
How does \(H\) work?
First it expands the state to 64 bytes as follows:
The first 4 bytes are a constant defined in the spec (Tao 0).
The next 16 bytes are the seed \(k\).
The next 4 bytes are another constant (Tao 1).
The next 8 bytes are the nonce.
The next 8 bytes are the index (the counter).
The next 4 bytes are a third constant defined in the spec (Tao 2).
The next 16 bytes are the seed again.
The final 4 bytes are a fourth constant (Tao 3).
We apply a function to these 64 bytes, we’ll call it \(h\). It’s a 1:1 function, mapping to another 64 bytes. It’s invertible, designed to be fast on x86.
It applies \(h\) 10 times, each time on its output.
Finally you do a word-by-word addition of the final output with the original input (ie 4 bytes at a time) and that’s the pseudorandomized output.
There are no significant attacks on this. It seems to be unpredictable. It’s very fast.
If you need a stream cipher use something like Salsa, one of the eStream finalists anyway.