Block Ciphers (Boneh)
Now going to cover block ciphers, the crypto work horse.
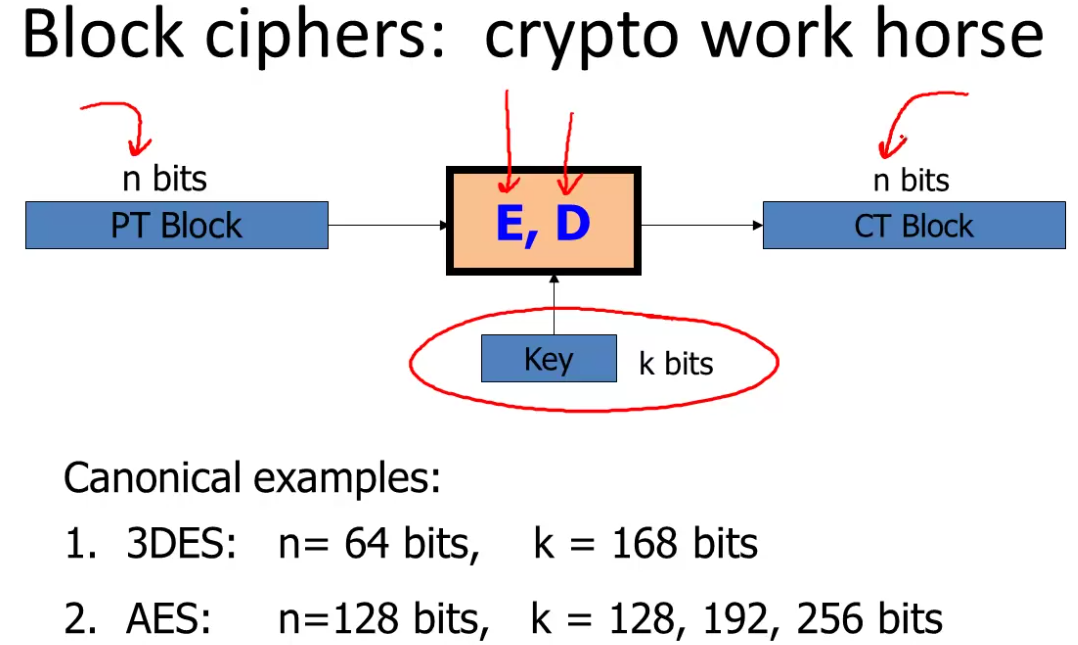
A block cipher is a pair of algorithms \((E,D)\) that take as input a k bit key, and an n bit block, and output an n bit block.
Two canonical examples: Triple Des (3DES), with 64 bit blocks with a 168 bit key.
More recent is AES, with 128 bit blocks, with variable sized keys (128, 192, 256), the longer the key the slower the algorithm, but presumably the more secure.
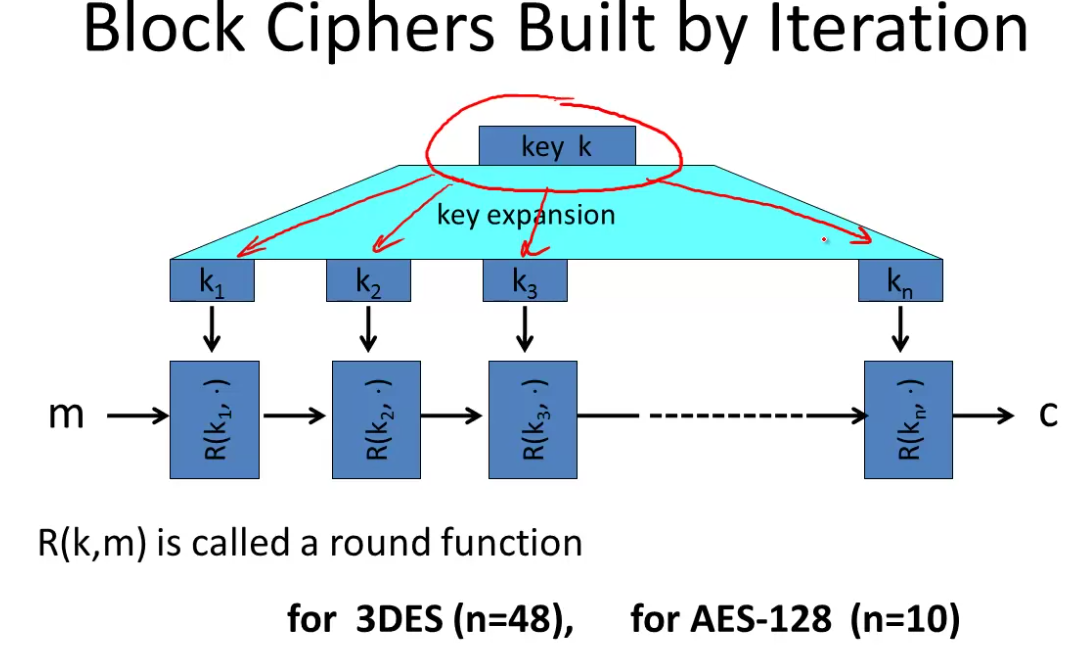
Block ciphers are built by iteration. You take the key k and expand it into a sequence of \(n\) keys, called round keys.
The cipher then iteratively encrypts the message again and again through each round key, using a round function:
Note that block ciphers are considerably slower than stream ciphers, but we can do more with them.
One of the goals here is to understand how to use block ciphers correctly.
To do this, we’ll abstract a little so we can reason about them. The abstraction we’ll use is a pseudo random function (PRF) and a pseudo random permutation (PRP).
A pseudo random function is defined over a key space, input space, and output space: \((K,X,Y)\)
it’s a function that takes a key and input as input, and returns an output from the output space.
The only requirement is that there is an efficient way to evaluate them.
A pseudo random permutation defined over a key space and a set \(X\): \((K,X)\).
The resulting function \(E\) It takes an element in the key space and an element in \(X\) and outputs an element in \(X\).
The function E should be easy to evaluate, and deterministic.
The function \(E(k,\cdot )\) is one-to-one. So given a key, every element in \(X\) is mapped to exactly one element in \(X\).
As such it’s invertible, and there exists an efficient inversion algorithm \(D(k,y)\).
We’ll use pseudo-random permutation and block cipher interchangeably.
So AES is a PRP \(K \times X \rightarrow X\) where \(K = X = \{0,1,\}^{128}\)
And 3DES is also a PRP where \(X = \{0,1\}^{64},\; K= \{0,1\}^{168}\)
Functionally any PRP is also a PRF. A PRP is a PRF where X=Y and is efficiently invertible.
Secure PRFs
What is it for a PRF to be secure?
Let \(F: X \times K \rightarrow Y\) be a PRF.
Let \(Funs[X,Y]\) be the set of all functions from X to Y. This will be a large set.
Let \(S_F = \{ F(k,\cdot ) | k \in K \} \subseteq Funs[X,Y]\)
We fix the key k, let the second argument float, and that defines the function.
We say that a PRF is secure if a random function in \(Funs[X,Y]\) is indistguishable from a random function in \(S_F\).
IE a random function should be indistinguishable from a pseudorandom function.
A simple example of a broken algorithm: Let the algorithm output 0 if the input is 0, otherwise a genuinely random output. This is enough to break the algorithm and mean it’s insecure since we have a known output to one input.
From PRF to PRG
We can easily get a pseudo random generator from a PRF.
Let our PRF output \(\{0,1\}^n\) bits.
Let our generator take an input k and output the following:
\[G(k) = F(k,0) || F(k,1) || \dots || F(k,t)\]
We now have \(n \times t\) bits, pseudo randomly generated.
Note this is parallelizable - we can compute the odds and evens on different cores for example. This is an advantage over stream ciphers we looked at earlier.