3DES (Triple-Des)
Data Encryption Standard (DES)
Early 70s, IBM started a crypto group, and produced a cipher called Lucifer.
1973, NBS asks for block cipher proposals, IBM submits variant of Lucifer.
1976, NBS adopts DES as federal standard - reduced key length to 56 bits, block length to 64 bits.
1997, DES broken by exhaustive search.
2000, NIST adopts Rijndael as AES to replace DES.
Banks use DES for integrity in bank clearing house systems. Was the main encryption standard for the web for a long time.
Core idea is a Feistel Network:
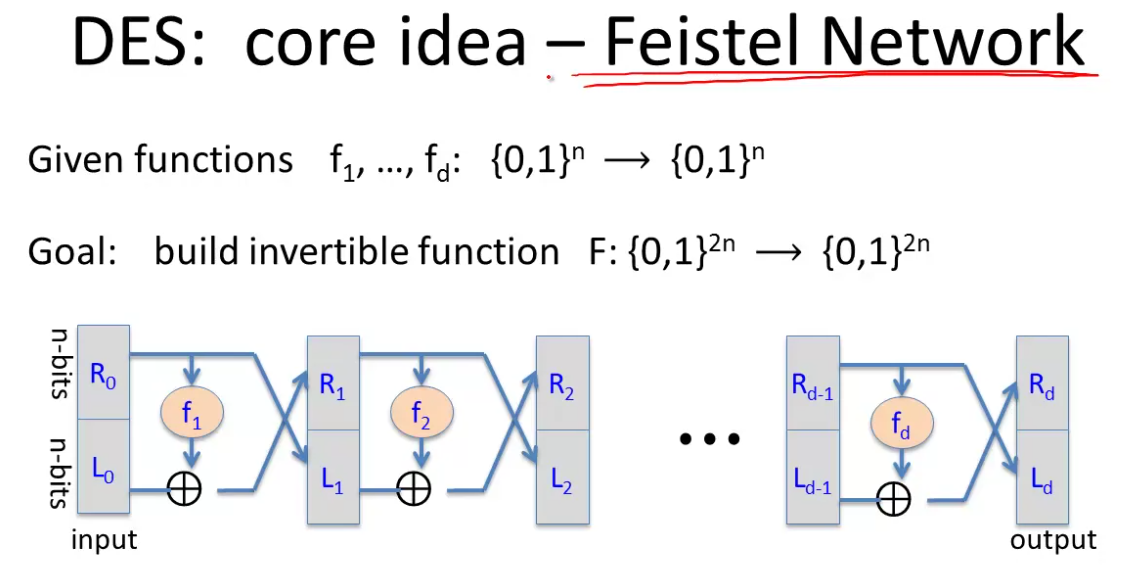
R and L stand for Right and left.
The claim is that even if the functions themselves aren’t invertible, the overall network is invertible.
This is easily seen by constructing the inverse of a step.
The circuit then is the same for encryption or decryption. The functions are just applied in inverse order.
DES is a 16 round Fesitel network, with each function mapping 32 bits to 32 bits.
\(k_i\) is a round key derived from the 56 bit input key.
The key thing is that the functions must not be linear, otherwise you can reverse engineer the whole thing.
Exhaustive Search and Triple-DES
Our goal in exhaustive search is, given a few input output pairs from a cipher, to find the key that maps the two.
Note as an aside that the probability of a collision (two keys producing the same cipher text for a plain text message) is very low. Take a truly random mapping, in 64 bit space the probabilty of a collision is the sum of the probabilities of all other keys. So with a 56 bit key you get \(2^{56} \cdot \frac{1}{2^{64}} = \frac{1}{256}\) so the probability of uniqueness is \(1 - \frac{1}{256} = 99.5%\)
With two keys, you repeat the analysis and get even closer to 1. So two input/output pairs are enough for exhaustive key search.
By 1999 DES could be cracked in 22 hours.
So 56 bit ciphers should not be used.
Strengthening DES - one method is Triple-DES.
We define a block cipher as \(E: K \times M \rightarrow M\) and then \(3E: \; K^3 \times M \rightarrow M\) as:
\[3E\left( (k_1,k_2,k_3), m \right) = E \left( k_1, D \left( k_2, E \left( k_3,m \right) \right) \right)\]
Why EDE rather than EEE, it’s a hack so that if you have a hardward implementation of triple-des you get an implementation of single DES for free by setting all three keys as the same.
Now our key size is 168 bits. Unfortunately it’s now three times slower.
Why not double DES? Doubling the keyspace already protects against exhaustive search, but it’s vulnerable to a meet in the middle attack.
This is because the following:
\[E(k_1, E(k_2, m)) = C\]
Can be re-written as follows by applying the decryption algorithm to both sides:
\[E(k_2,m) = D(k_1, c)\]
We can attack this by mapping both sides to the value in the middle. We do an exhaustive search on both directions to see where they meet.
The same attack on triple DES still takes a long time.
Additional Attacks
There are a vast number of attacks on block ciphers, never build your own!
Side channel attacks - measure tiem and power for enc/dec you can read the cipher
Fault attacks - errors in the last round can expose the secret k.
Use libraries!
Another DES attack exploits that a tiny bit of linearity in the 5th S-box of DES led to a much faster attack than exhaustive search.
Another theoretical attack - quantum computing. If you imagine a functiont that outputs 1 if \(E(k,m) = c\) and 0 otherwise, this is a hard problem for traditional computers to solve,
But quantum computers can solve it in root \(|K|\) time. This breaks DES and AES-128. If quantum computing is real, move to 256 bit keys.