Message Authentication Codes (MACs)
In message integrity our goal is to provide integrity, not confidentiality.
For example we want to protect public binaries on disk, or banner ads on pages. Users don’t care about confidentiality here, but they do care about integrity.
The basic method of providing message integrity is a MAC a Message Authentication Code.
It works as follows:
Alice and Bob share a secret key, unknown to the attacker.
Alice ‘signs’ her message using a MAC signing algorithm, \(S\) which outputs a tag: \(\textrm{tag} \leftarrow S(k,m)\)
The tag is short, even if the message is gigabytes long, the tag will be short, say 90 bits.
Bob then runs the Mac verification algorithm which outputs a pass/fail: \(V(k,m,tag) = \textrm{yes}\)
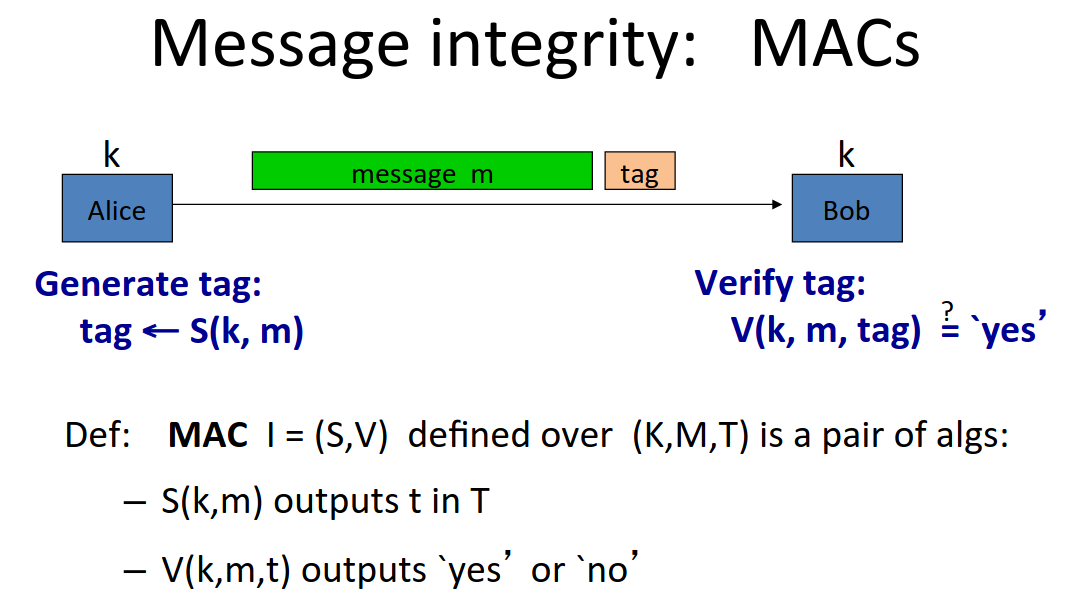
There is the consistency constraint on \(S,V\):
\[\forall k \in K, \forall m \in M: V\left(k,m,S(k,m) \right) = \textrm{yes}\]
Integrity must have a shared secret key.
For example CRC is a common integrity algorithm without a secret key. It simply takes as input a message and computes a tag, which is then used to verify the message.
This is only intended to catch random errors not malicious ones. An attacker can just man in the middle, intercept the message and tag, and replace them. CRC is not intended to defend against this and should not be used in this way.
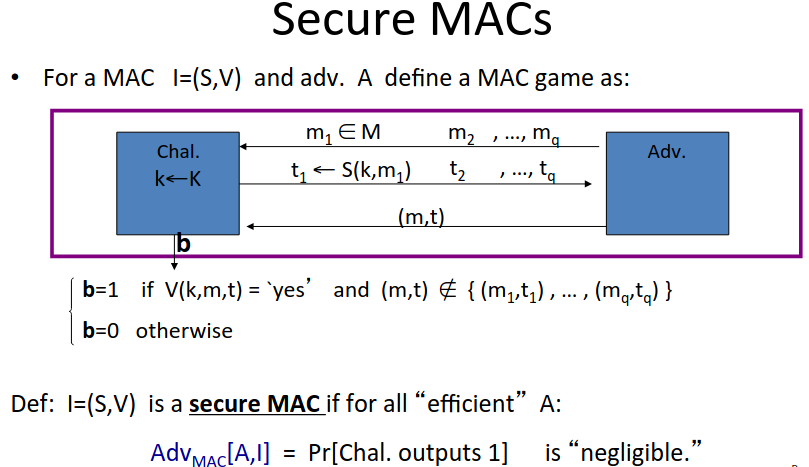
MAC Security
What is it for a MAC system to be secure.
The attacker’s power will be a chosen message attack.
for \(m_1, \dots , m_q\) attacker is given \(t_i \leftarrow S(k,m_i)\)
Attacker’s goal is existential forgery: produce a new valid pair \((m,t)\)
Security requires that the attacker cannot produce a valid tag for a new message, and that given \((m,t)\) the attacker cannot produce \((m,t’)\) where \(t \neq t’\).
Here’s the game in this instance:
Note that this game has the following implications:
A MAC which outputs the same tag for two different messages with a probability of 0.5 is not secure. Since the attacker can output \(m_0\), receive the tag, then output \(m_1\) and with probability 0.5 the tag will be valid.
A MAC with a tagspace \(\{0,1\}^5\) is not secure. The attacker can just guess and has a \(\frac{1}{2^5}\) chance of getting it correct.
Typical tag length is 64,96, or 128 bits. (TLS uses 96 bits). So the advantage from guessing is just \(\frac{1}{2^{96}}\) which is negligible.
MACs can be used to protect files from tampering as follows:

Note that to protect against swapping files the file name (path) has to be part of the content signed by the MAC. MACs generally don’t protect against swapping valid content/signature pairs.
MACs based on PRFs
Note that any secure pseudo-random function gives us a secure MAC.
The tag space still needs to be large enough to defend against random guessing.
If the output of the PRF is large, then we’re good.

So now we know that a secure PRF is a secure MAC, we have our first MAC already - AES is a MAC for 16-byte messages.
This gives us the first main question too - if we have a MAC for small inputs, how do we convert it into a MAC for large inputs?
There are two main constructions used in practice:
CBC-MAC used in banking (ANSI X9.9, X9.19, FIPS 186-3). Used in automatic clearing house.
HMAC used in internet protocols: SSL, IPsec, SSH)
Both convert a small PRF into a big PRF. Both can be instantiated by using AES as the underlying cipher.
Notes as part of this that truncating MACs based on PRFs is still secure. If \((S,V)\) is a MAC based on a secure PRF outputting n-bit tags, the truncated MAC outputting w-bit tags is secure as long as \(\frac{1}{2^w}\) is still negligible (eg \(w \geq 64\)).
Truncating doesn’t give the attacker any more info, on the contrary they lose info.