CBC-MAC, NMAC, PMAC

Our goal is to construct a PRF for long messages given a PRF for short messages (AES).

ECBC: Encrypted CBC-Mac

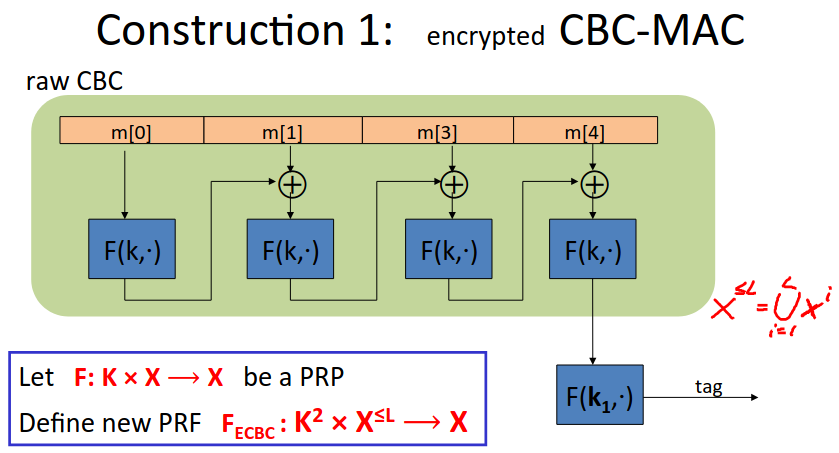
Here \(X\) is \(\{0,1\}^n\) where \(n\) is the number of bits in the block size of the underlying PRF (eg 128 bits for AES).

So our MAC takes pairs of keys and arbitrarily long messages, and outputs a tag of the size of the underlying block.

Here we’re running through the CBC chain, except we don’t output the intermediate values.

Note the last step - the output of the CBC chain is encrypted using an independent key.

Without that last step we have ‘Raw-CBC’, but that is not a secure MAC. Many products do this incorrectly.

We can truncate the tag so long as the length still satisfies non-neglibitilty.

NMAC

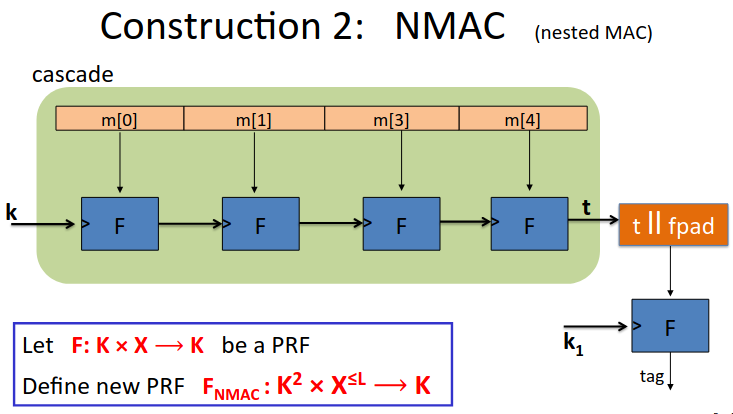
Note here the output of the PRF is in the keyspace, not the message space.

So the chain generates a new key each round.

Note if you stop before the final orange step you have a cascade function and this is not secure.

We have to map the output of the set K from the cascade function into the set X.

This is used when the block length is much bigger than the key length.

We append a fixed pad (fpad) to the output, this is then run through a final encryption step, again with an independent key, to give us our final output tag (again in the key space).

The reason we do this is that without it, I can just feed a single message into the cascade function, and from there generate an existential forgery for the original message concatenated with any arbitrary message. I can just apply the underlying function to the original output. This is called an extension attack.

Note that you have to change the key after \(|Y|^{\frac{1}{2}}\) messages. Given the birthday paradox we’ll find a collision with reasonably high probability. Once we’ve found a collision we can then create a fake tag. We run one through the tag with a message concatenated. The tag will be the same as running the collided message with the same concatenation. So with AES change the key after \(2^{48}\).

ECBC-MAC is commonly used as an AES-based MAC. CCM encryption mode used in 802.11i. NIST standard called CMAC.

NMAC not usually used with a block cipher like AES or 3DES, need to change AES key on every block, requires re-computing AES key expansion. Typically use a block cipher that’s better at changing key each block. NMAC is the basis of the popular HMAC however.

Mac Padding

What do we do when the message length is not a multiple of the block size?

We can’t pad with 0, since then we can get the tag for m || 0 too and mount an existential forgery.

Padding must be invertible - we should not have a collision on the padding.

ISO suggested just padding with 1000…00. Add a new dummy block if needed. Lots of products don’t add the dummy block and then the MAC is insecure.

A variant without adding a padding block is a randomized pad used in CMAC, a variant of CBC-Mac using a third key.

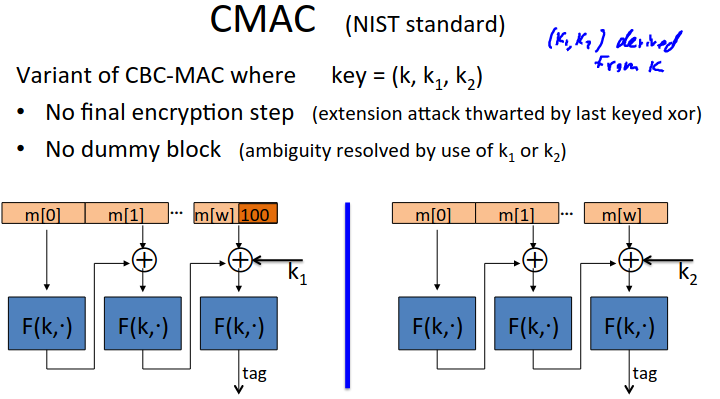
The keys \(k_1,k_2\) are derived from \(k\) with a PRG.

If the message is not a multiple of the block length then we append ISO padding and XOR with \(k_1\), otherwise we don’t pad and use \(k_2\) to XOR.

The attacker now can’t do the extension attack, since it doesn’t know the last block. So we don’t do the final encryption step, or add a dummy block.

PMAC: A Parallel Mac

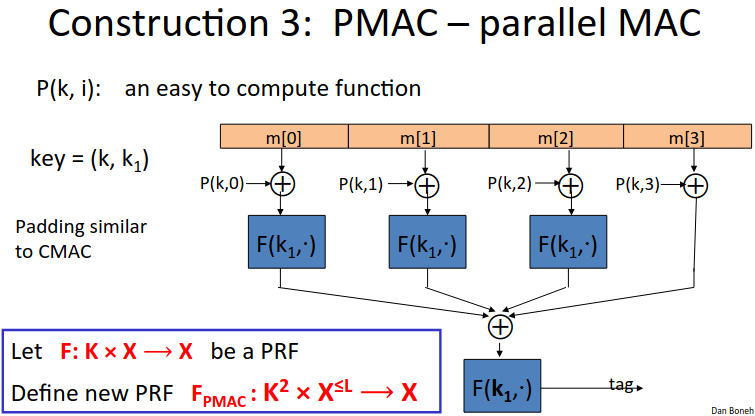
We feed each block into an xor with a value computed based on the key and the block sequence (without this you could arbitrarily swap message order). Then you run through the PRF, xOR all the results, and do a final encryption step.

The function of P is an easy to compute function, and is enough to ensure security.

The pair of keys feeds this masking function and the PRF.

One aspect of PMAC - you can increment the tag for a long message if a small part changes if the underlying PRF is a PRP (invertible).

One Time MAC

Analogue of a one time pad.

Note we can get a many-time-mac from a one-time-mac by taking the one-time mac result from a key, and xOR it with a one time pad (a PRF on another key and a nonce).

This is Carter-Wegman MAC The advantage is the large message is encrypted with a fast algo, while the slow PRF is run over its smaller output.