Collision Resistance

Introduction

Let \(H: M \rightarrow T\) be a hash function where \(|M| » |T|\)

A collision for \(H\) is a pair \(m_0,m_1 \in M\) such that: \(H(m_0) = H(m_1)\) and \(m_0 \neq m_1\)

A function H is collision resistant if for all explicit efficient algorithms \(A\):

\[\textrm{Adv}_{\textrm{CR}}[A,H] = Pr[A \; outputs \; collision \; for \; H]\]

is ‘negligible’.

example: SHA-256 (outputs 256 bits).

IE we know there are lots of collisions, since the input space is much bigger than the output space. The question is whether it’s possible to find these collisions efficiently.

From collision resistance we can get MACs fairly straightforwardly:

Note this is only secure given collision resistance.

Here’s a direct application of collision resistance: ‘signing’ public data.

Let’s say I want to distribute a software package on the internet. I create a read-only public space with the hash of the package. Then the user can download the package, hash it, and compare the hashes.

Note this is the complement of the MAC approach to this, where we needed a secret key to verify the integrity. Here we don’t need a key to verify, but we need a read-only public space.

This pattern is common, eg in Linux distribution.

Generic Birthday Attack

There’s a generic attack on hash functions that forces them to have a lower output bound.

uniform distribution is the worst case for the birthday paradox, and there we have a probability of a half if we choose 1.2 x root length of set.

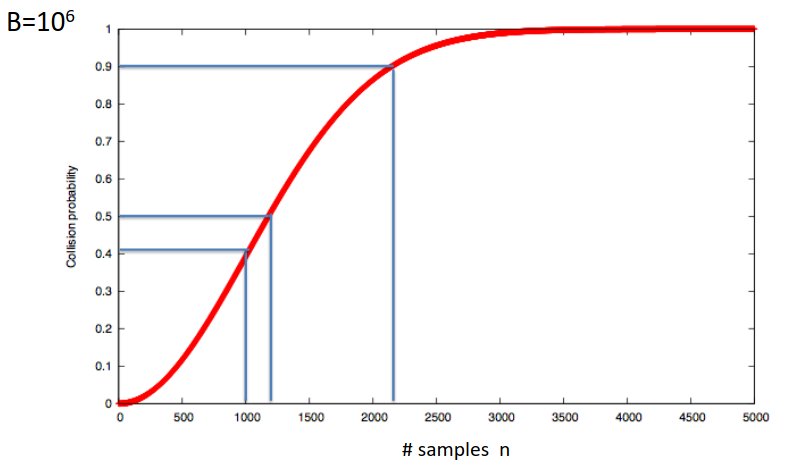
This is why SHA-1 is no longer considered secure, it is vulnerable to collisions though no one has found one yet.

Don’t use SHA-1, use SHA-256.

Merkle-Damgard Paradigm

All collision resistant hash functions follow a general paradigm:

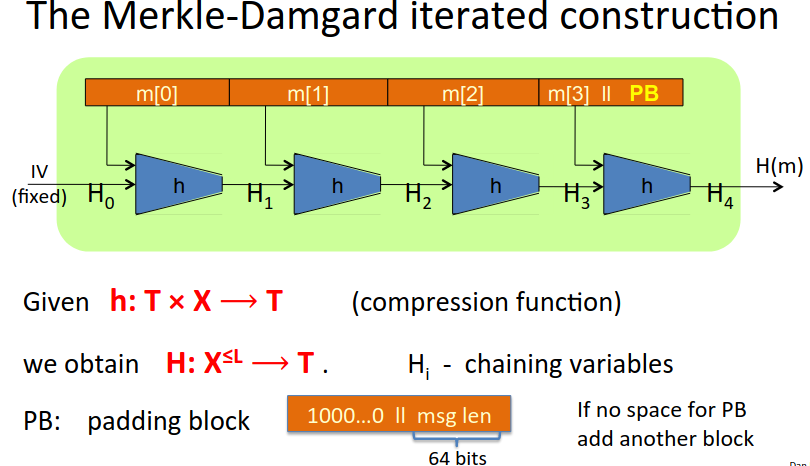
There is a fixed IV embedded in the standard.

We take a large message m, divide it into blocks, and feed it through a hash function (compression function), initially with the IV, and then feed the resulting chaining variable through the next steps for the rest of the message blocks.

The paradigm is popular because of the theorem that if the little function \(h\) is collision resitant, then so is \(H\).

Constructing Compression Functions

We can construct a compression function from a block cipher as follows:

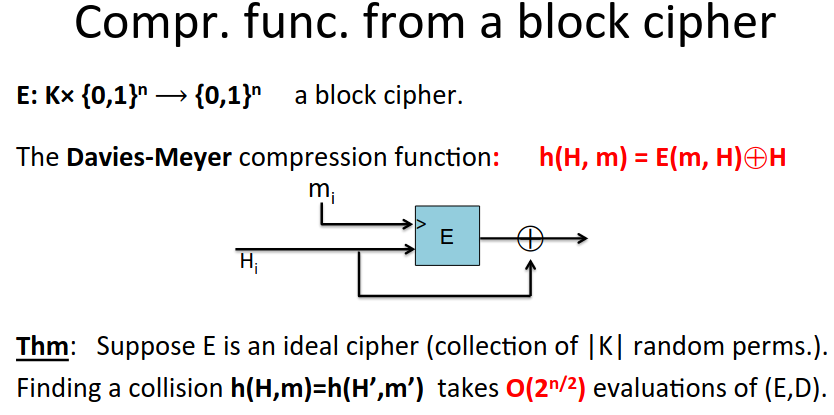
This is as collision resistant as possible!

SHA functions always use Davies-Meyer.

There are many variants, some secure, some insecure.

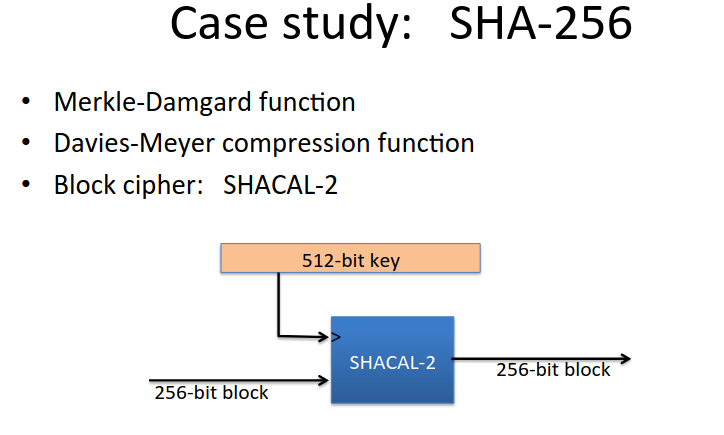
SHA-256

We have all the elements now of SHA-256: