Deterministic Encryption
Deterministic encryption will always map the given message to the same cipher text. (no nonce).
Comes up a lot in practice - eg if you want to store encrypted data in a database. All the db sees is encrypted data, but the server can retrieve records if the encryption is deterministic.
But we know that deterministic encryption cannot be CPA secure. Since if we see the same cipher text twice we know the messages are the same.
The solution is to restrict the type of messages that can be encrypted, such that the encryptor never encrypts the same message twice. In this way the pair \((k,m)\) never repeats.
This happens when the encryptor chooses messages at random from a large message space (eg we encrypt keys).
Or when the message structure ensures uniqueness (eg unique ID).
A common mistake in practice is to use CBC with a fixed IV. But this is not deterministic CPA secure. Neither is CPT with fixed IV.
So how do we construct a secure Deterministic Encryption solution?
Synthetic IV: Deterministic Authenticated Encryption
Let \((E,D)\) be a CPA-secure encryption where \(E(k, m; r) \rightarrow c\).
\(r\) signfies the random element that gives the cipher CPA security.
Now let \(F: K \times M \rightarrow R\) be a secure PRF that outputs strings that can be used as randomness.
Then we define \(E_{det} ((k_1,k_2), m)\)
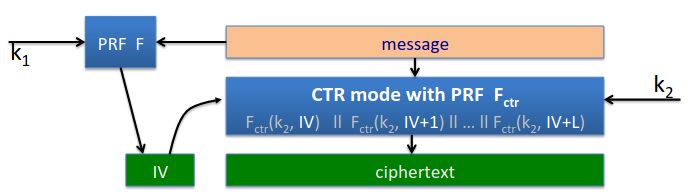
First we use \(k_1\) to derive the random string, using \(F\): \(r \leftarrow F(k_1,m)\)
Then we encrypt m using the randomness it derived: \(c \leftarrow E(k_2, m; r)\)
Then we output \(c\).
Now if we encrypt the same message several times we’ll generate the same cipher text.
Well suited for messages longer than one AES block.
This gives us ciphertext integrity for free. This gives us deterministic authenticated encryption.
Here’s the encryption step, using CTR mode - cipher is counter mode with random IV:
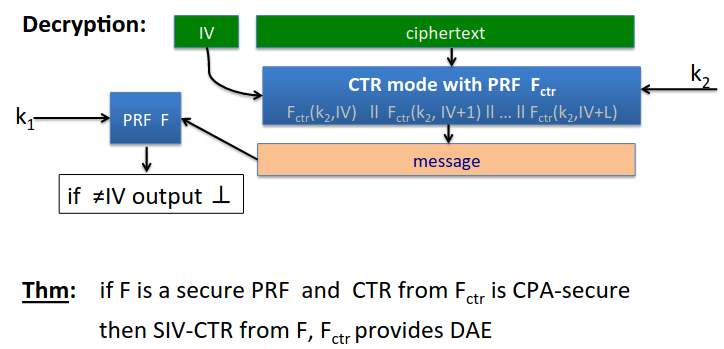
Now in the decryption step we add one more check, we apply the same PRF to the message, and we should get the same IV as the sender supplied:
PRP
If messages are short (say less than 16 bytes) there’s a better method, we can just use a PRP.
All the attacker sees, if messages are distinct, is random distinct values in \(X\). Distributions are identical, so attacker cannot distinguish.
We can just use AES, this is deterministic CPA secure. But no integrity here.
Can we use this on larger messages?
There is a standard mode called EME that will construct a PRP based on a smaller space for an arbitrarily large space.
We can get authentication too very simply. We append 80 0s to the end of the message, and encrypt using our PRP. Then we we decrypt we look at the last 80 bits and reject if they are not 0.
This works so long as the number of 0s is large enough.