Tweakable Encryption

Motivating problem - disk encryption. We have no room for expansion, if the disk sectors are a fixed size then the cipher text must be that size.

So we must use deterministic encryption, no integrity bits. So all we can achieve is deterministic CPA security.

So every sector needs to be encrypted using a PRP.

But what do we do if the plain text is the same? EG if some sectors are empty.

We could try a different key for every sector. But then we do leak if a sector is changed and then reverted.

How do we manage keys? We can generate keys from a master key. Store the master key and then generate \(k_t = PRF(k,t)\), with t being a number from 1 to L (number of memory sectors).

Could we do better than that? Yes, with a tweakable block cipher

Tweakable Block Cipher

Goal: Construct many PRPs from a single master key \(k \in K\).

Syntax: \(E,D: K \times T \times X \rightarrow X\)

Then for every \(t \in T\) and \(k \rightarrow K\):

\(E(k,t,\cdot )\) is an invertible function on \(X\) indistinguishable from random.

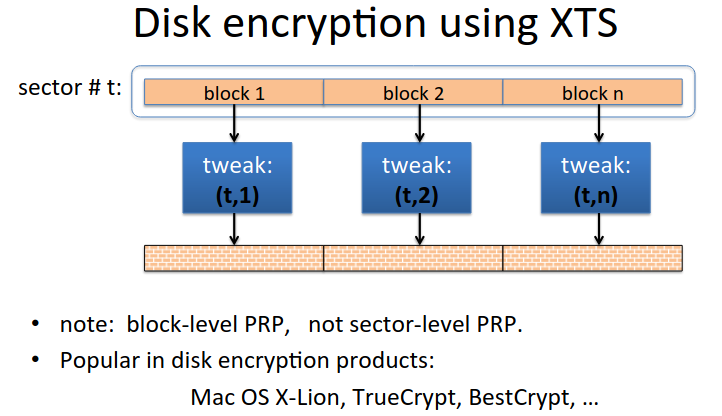
Application: use sector number as the tweak, gets its own independent PRP.

Here’s the naive implementation:

If we have a secure PRP \((E,D)\) where \(E: K \times X \rightarrow X\) and \(K\) and \(X\) are the same size.

Then the tweakable construction would be:

\[E_{tweak}(k,t,x) = E\left( E(k,t), x \right)\]

But this needs \(2n\) evaluations of E for encrypting \(n\) blocks.

There is the XTS construction which does better, twice as fast.

They are narrow block constructions, and how it is done in practice: