Key Exchange: Problem
We’ve seen how two users can share information securely with a shared key. Now the problem becomes, how do they agree this secret key in the first place?
Imagine every user having to store a key for each user they want to communicate with. Now we have to manage n keys per user.
One better way is a TTP - a Trusted Third Party
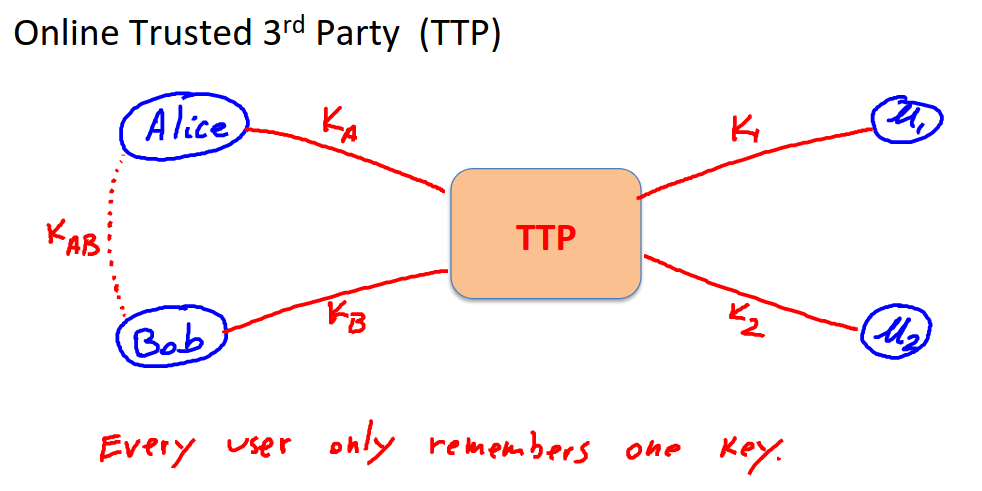
Now each user only stores one key, and they have unique keys that are shared between them via the TTP.
How do they agree the shared key?
Here’s a toy protocol:
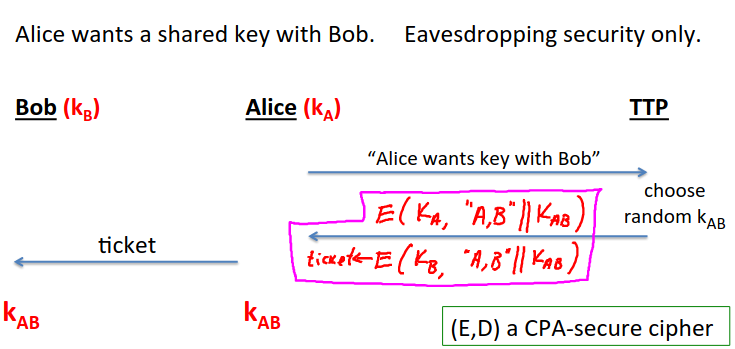
Here the TTP is needed for every key exchange, and knows all session keys.
This doesn’t make sense at web scale, but in the context of an organization where you could have a server operate as a TTP it could do.
Something like this is the basis of the kerberos system.
The toy version though is completely insecure against an active attacker, only secure against eavesdropping.
Key question: can we design shared key protocol without an online TTP.
The answer is yes, and this is the starting point of public-key cryptography.
There are three ideas for implementation covered in the course: Merkle (1974), Diffie-Hellman (1976), and RSA (1977).
There is more recent work (ID-based enc, functional enc.)
Merkle Puzzles
It turns out we can do key exchange without a TTP just using symettric encryption, but it’s very inefficient.
The main tool is a puzzle - a problem that can be solved with some effort.
EG find the secet key in a symmetric cipher where most of the message is 0.
Alice generates a lot of puzzles and sends them to Bob.
Bob picks one randomly, and solves the puzzle, discarding the others.
He sends the identifier for the puzzle back to Alice, and then stores the key contained in the puzzle, which they now share as a secret key.
So the attacker has to do \(n^2\) puzzles. The attacker can still break this, but takes them longer.
You could make it harder for the attacker, but that makes it harder for the participants.
So this isn’t used in practice.
We need more than general symmetric ciphers to improve this.