Public Key Encryption

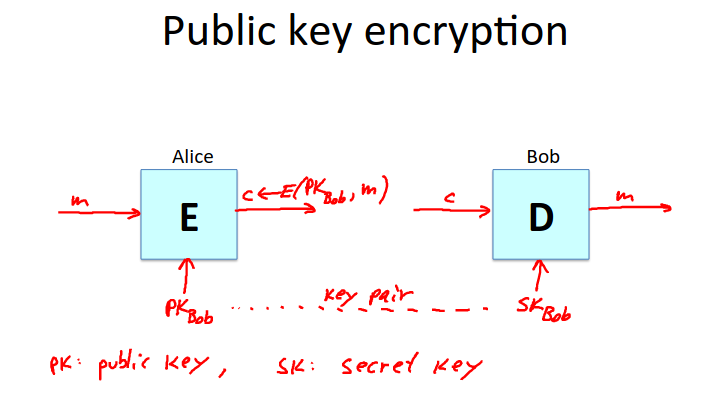
As with symmetric encryption, there is an encryption algorithm \(E\) and a decryption algorithm \(D\).

However here, the encryption algorithm is given a public key \(PK\), and the decryption algorithm is given a secret key \(SK\).

Together these keys form a key pair.

Definition

A public-key encryption system is a triple of algorithms: \((G,E,D)\)

\(G\) randomized algorithm outputting a key pair \((pk, sk)\)
\(E(pk, m)\) randomized algorithm that takes \(m \in M\) and outputs \(c \in C\)
\(D(sk, c)\) deterministic algorithm that takes \(c \in C\) and outputs \(m \in M\) or \(\bot\)

Consistency requirement:

\(\forall (pk,sk)\) output by \(G\):

\[\forall m \in M: \; D(sk, E(pk,m)) = m\]

We can establish a shared secret as follows:

Alice generates a \((pk,sk)\) pair.

She sends her public key to Bob.

Bob generates a random key \(k\) in the keyspace.

Bob encrypts \(k\) using Alice’s public key and sends it to Alice.

Alice decrypts with her secret key.

\(k\) is now a shared secret key.

Note that this protocol now has a sequence order, unlike DH.

Again this protocol is completely insecure against man in the middle attacks.