RSA Trapdoor Permutation

RSA is an example of a trapdoor function (see Public Key Security from Trapdoor Permutations)

Note they’re permutations because the domain and co-domain are the same set.

Recall the mod composite rules discussed earlier:

RSA Trapdoor Permutation

Published in 1977, used extensively ever since - used in TLS, email, file systems, many others.

Key Generation

Choose random primes \(p,q\) approx. 1024 bits. Set \(N=pq\)

Choose integers \(e,d\) s.t. \(e \cdot d = 1 \pmod{\phi (N)}\)

ouptut: \(pk = (N,e)\), \(sk = (N,d)\)

\(e\) is often called the encryption exponent and \(d\) the decryption exponent .

Trapdoor Function

\(F(pk, x): \mathbb{Z}_N^* \rightarrow \mathbb{Z}_N^*\) ; \(RSA(x) = x^e\) (in \(Z_N\) ).

\(F^{-1}(sk,y) = y^d\); \(y^d = RSA(x)^d = x^{ed} = x^{k \phi (N) + 1} = \left( x^{\phi (N)} \right)^k \cdot x = x\)

Why is this function secure? The assumption is that RSA is one-way.

Now we can plug the RSA trapdoor permutation into the ISO standard.

Never use RSA directly on the message (ie never do \(c := m^e\) and decrypt with \(c^d\)). This is often how RSA is described in the textbooks, but this is NOT SECURE, for reasons explained in prior segment.

RSA is a trapdoor permutation not an encryption scheme!

Here’s an attack on the textbook RSA in a web server context:

PKCS 1

The ISO standard version is not often used in practice.

In practice we typically get a shared key (eg AES key, c. 128 bits), and a message, then do some pre-processing to take the key to the size of \(N\), and then apply RSA, like this:

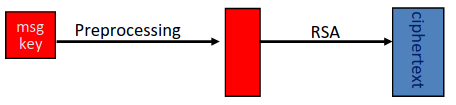
This begs the question, how do we pre-process (how to expand the key) and how is it secure?

Here’s one way of doing it, widely used in practice - known as PKCS1 v. 1.5.

This is mode 2 (encryption) - mode 1 being signature.

So we set the message (the AES key for example) as the least significant bits.

then separate with FF (16 bits of 1)

then append random pad which does not have FF within it.

Finally at the MSB you put the number 02, which indicates mode 2.

This whole value is then RSA encrypted.

The decryptor will decrypt the whole thing, remove the 02, remove the random pad until FF, remove FF, and then have the AES key.

This is used in HTTPS.

Turns out this is vulnerable, there was no security proof.

Attackers could repeatedly query HTTPS servers to learn whether the MSB is 02 or not, a million queries were enough to decrypt the whole message from this info.

A minor change was introduced (if the padding is invalid, fake it) and made the algorithm more secure. But is there a better way?

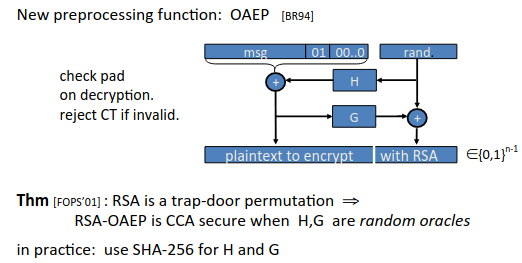
OAEP

Optimal Asymmetric Encryption Padding or OAEP was introduced as an improvement to v. 1.5 of PKCS.

PKCS1 v. 2 now supports OAEP.