Public Key Encryption from Diffie Hellman

Recall that public key encryption is used in a variety of settings.

In key exchange - server gives client its public key. Client encrypts secret using public key, server decrypts secret using private key. Now we have a shared secret.

In non-interactive settings: Secure email - Alice encrypts message to Bob using Bob’s public key. Only Bob can decrypt.

File encryption:

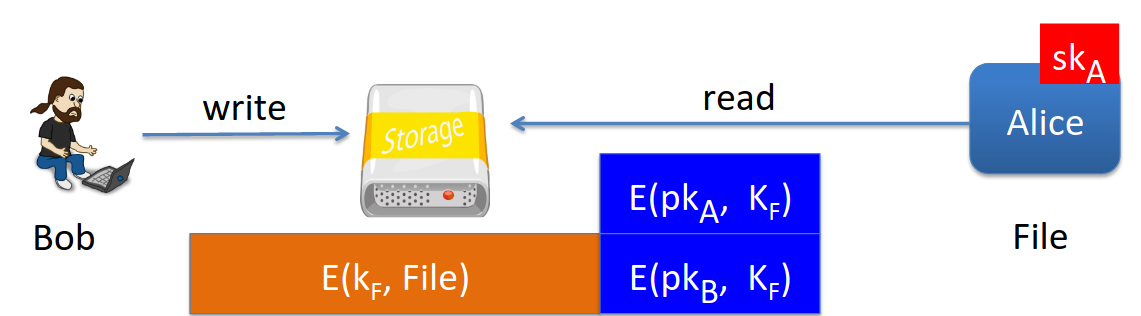
Bob wants to store encyrpted file. He generates a random key \(k_F\) that is used to encrypt the file. Then he encyrpts the random key itself using his own public key - \(E(pk_B, k_F)\) - which is used as a header to the encrypted file or similar mechanism.

Now Bob can decrypt the file at any point using his secret key - he first decrypts the header key \(k_F\) and then uses that to decrypt the file itself.

If Bob wants to give access to anyone else he will decrypt \(k_F\) using their public key.

Key escrow:

Data recovery without Bob’s key. Mandatory feature in corporate environments.

Imagine Bob writes data somewhere using his key, then he’s fired or otherwise unavailable.

The corporation needs to access the files without Bob.

We do this through a key escrow service.

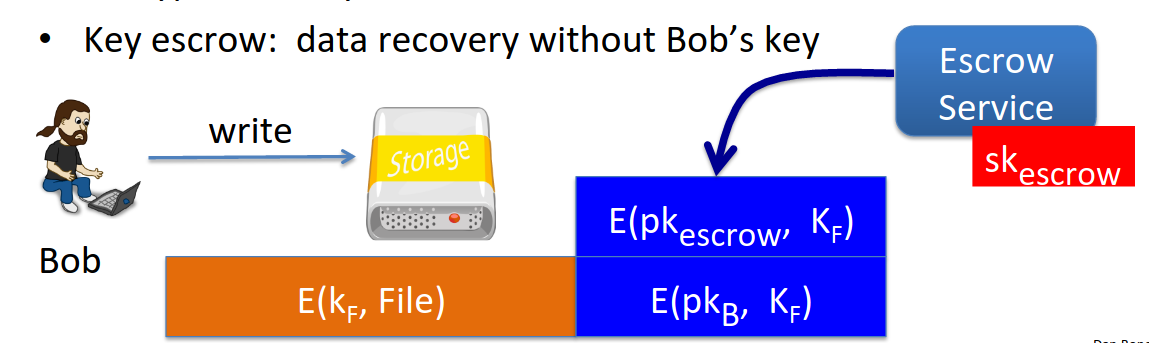
So we encyrpt the key using the escrow authority’s public key. If Bob disappears we can ask the escrow service to decrypt using its private key and recover the one-time key used to encrypt the file.

Diffie Hellman Constructions

We’ve looked at encyrption from trapdoor functions like RSA, now we’ll look at those based on Diffie-Hellman. They’re generally called ElGamal encryption schemes after their originator (student of Hellman’s).

ElGamal is used in GPG email encryption.

Recap of DH protocol:

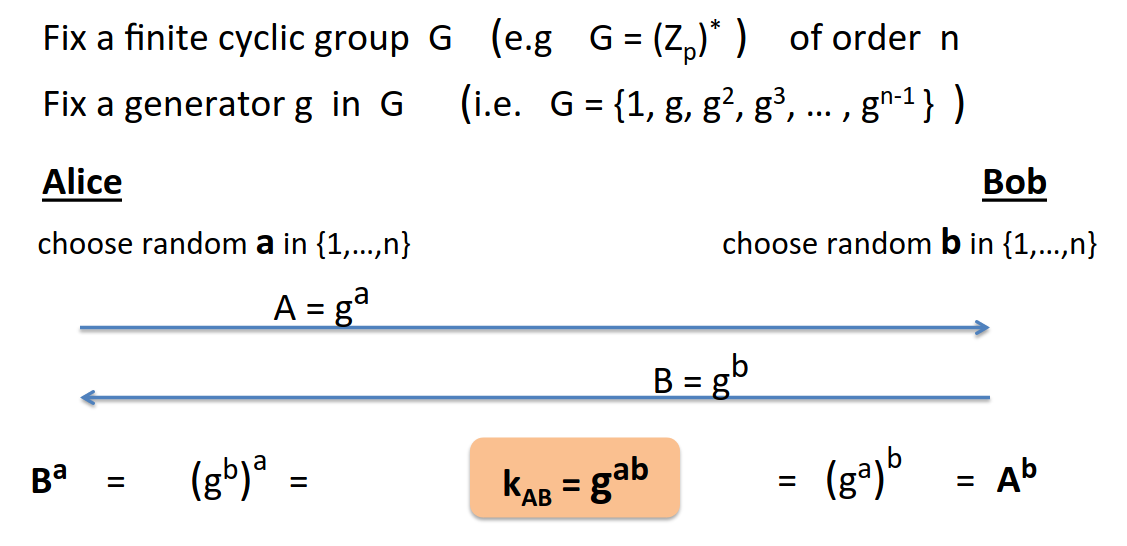
Here’s the intuition of how you convert this into a public key encryption scheme:

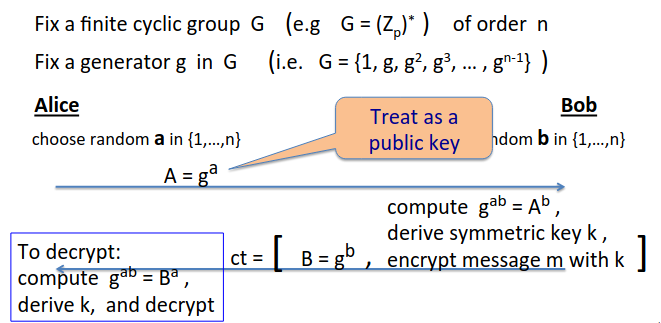
Slightly more formally,

We start with the following elements:

• \(G\) a finite cyclic group of order \(n\)

• \((E_S, D_S)\) Symmetric authenticated encryption defined over \((K,M,C)\)

• \(H: G^2 \righarrow K\) A hash function.

Then we construct a public key encyrption scheme \((Gen, E, D)\) as follows:

Gen:

• Choose a random generator \(g \in G\) and random \(a \in Z_n\)

• Output \(sk=a\), \(pk = (g,h=g^a)\)

E:

D: